3.1: Introducing Common Fractions
Chapter 3: Learning Outcome
By the end of this chapter, you should be able to:
- Write fractions as decimals and decimals as fractions.
- Add, subtract, multiply and divide rational numbers.
- Use order of operations.
- Graph rational numbers on the number line.
This section gives you the background details needed for working with common fractions.
Parts of Common Fractions
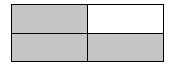
Common fractions are written with two numbers, one above the other, with either a straight or slanted line in between. The straight-line style is the one used most (see Figure 3.1.1).
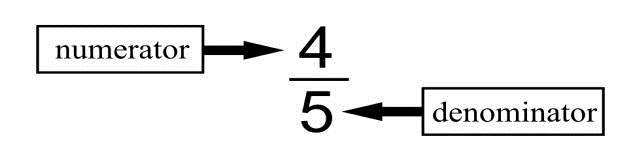
The denominator is the bottom number. It tells how many equal parts are in the whole thing. The numerator is the top number. It tells how many of the equal parts we are dealing with.

The whole thing is the bunch of bananas (see Figure 3.1.2). The whole thing has 5 equal parts (the bananas). The denominator is 5.
How many bananas have been eaten? 1
What fraction of the bananas have been eaten? [latex]\boldsymbol{\dfrac{1}{5} \text{ of the bananas}}[/latex]

The whole thing is a carton of one dozen eggs (see Figure 3.1.3). One dozen has 12 equal parts, so if we are talking about the carton, the denominator is 12.
How many eggs are still in the carton? 7
What fraction of the eggs are left? [latex]\boldsymbol{\dfrac{7}{12}\text{ of the eggs}}[/latex]
A fraction is always looking at things as parts of a whole. In the previous example of the eggs, the whole is 12 eggs. The part is the 7 eggs that are left. 7 is part of the whole of 12.
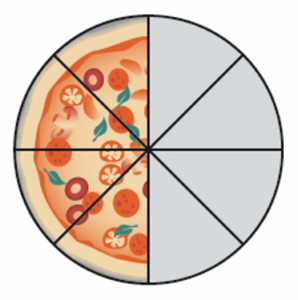
This pizza is one whole pizza (see Figure 3.1.4). The pizza is cut into 8 pieces. This means the whole is 8. How many parts are left? (The pieces that are shaded are the ones left.) Write a fraction of how many pieces of pizza are left.
The amount left over can be shown as a fraction: [latex]\dfrac{4}{8}[/latex]
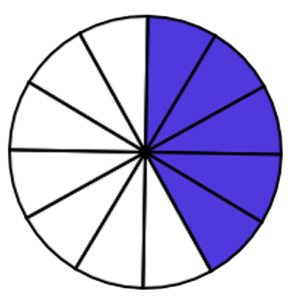
It is Peter’s 82nd birthday. There were 7 people, including Peter, at the party. Everyone wants a small piece of cake, so Kathleen cut the cake into 12 equal parts (see Figure 3.1.5). This means the whole is 12. There will be some left over.
The amount left over can be shown as a fraction: [latex]\dfrac{5}{12}[/latex]
Example E
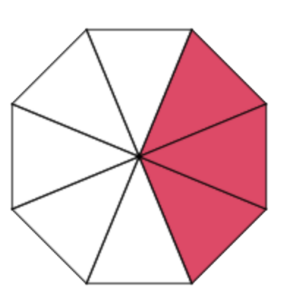
Sue made a strawberry pie to share with her family of 5. The pie was cut into 8 equal parts. This means the whole is 8. The kids are excited because there will be parts left over.
The fraction showing what amount of pie is left is: [latex]\dfrac{3}{8}[/latex]
Exercise 1
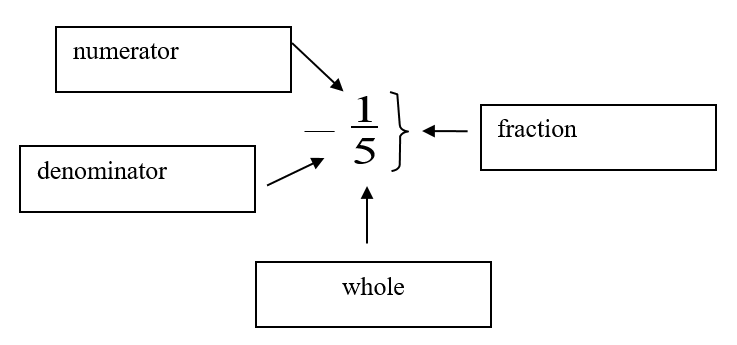
Look at the fraction below. Fill in the blank labels in Figure 3.1.7 with the four terms you are given:
Exercise 1 Answers
Writing Common Fractions
Exercise 2
Each shape drawn here is a whole. The shapes have been divided into parts.
- Ask yourself, “How many equal parts in the whole?” That number is the denominator.
- Count the number of parts that are shaded; that is the numerator.
- Write the common fraction to describe the shaded portion of each shape.
Example:

- How many parts make the whole? 4
- How many parts are shaded? 3
- Fraction: [latex]\boldsymbol{\dfrac{3}{4}}[/latex]
-

Figure 3.1.10 - How many parts make the whole?
- How many parts are shaded?
- Fraction:
-

Figure 3.1.11 - How many parts make the whole?
- How many parts are shaded?
- Fraction:
-
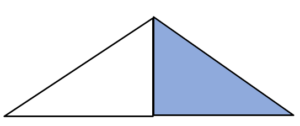
Figure 3.1.12 - How many parts make the whole?
- How many parts are shaded?
- Fraction:
Exercise 2 Answers
- Square.
- 4
- 3
- [latex]\dfrac{3}{4}[/latex]
- Rectangle.
- 8
- 5
- [latex]\dfrac{5}{8}[/latex]
- Rectangle.
- 5
- 2
- [latex]\dfrac{2}{5}[/latex]
- Triangle.
- 2
- 1
- [latex]\dfrac{1}{2}[/latex]
Exercise 3
Now, let’s draw some fractions.
Example: Draw the fraction [latex]\dfrac{1}{2}[/latex] in a circle (see Figure 3.1.13):
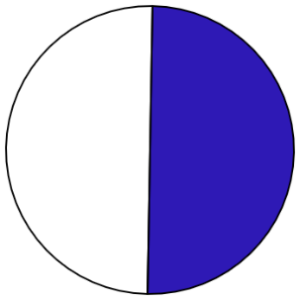
- Draw [latex]\dfrac{1}{4}[/latex] in a circle:
- Draw [latex]\dfrac{1}{3}[/latex] in a circle (here is a hint below):
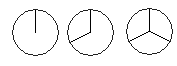
- Draw [latex]\dfrac{1}{2}[/latex] in the rectangle:

- Draw [latex]\dfrac{2}{4}[/latex] in the rectangle:

- Draw [latex]\dfrac{4}{8}[/latex] in the rectangle:

- What do you see in common with the three last boxes you just drew?
Exercise 3 Answers

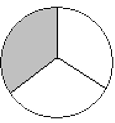



- All the shaded spaces are equal
Reading Common Fractions
You can read fractions in a few different ways:
- [latex]\dfrac{1}{2}[/latex] can be called:
- one over two
- one half
- [latex]\dfrac{1}{4}[/latex] can be called:
- one over four
- one fourth
- one quarter
- [latex]\dfrac{3}{4}[/latex] can be called:
- three over four
- three fourths
- three quarters
- [latex]\dfrac{1}{3}[/latex] can be called:
- one over three
- one third

Reading Numerators & Denominators
Remember: The numerator is read as a number.
The denominator is read with a special ending at the end of the numeral. The ending is usually th or ths as it was in decimals, but sometimes we use a different word. These are called ordinal numbers (see Table 3.1.1).
| If the Denominator Is… | Read… |
|---|---|
| 2 | half |
| 3 | third |
| 4 | fourth or quarter |
| 5 | fifth |
| 6 | sixth |
| 7 | seventh |
| 8 | eighth |
| 9 | ninth |
| 10 | tenth |
| 22 | twenty-second |
Add the “s” if the numerator is 2 or more. So [latex]\tfrac{2}{3}[/latex] is read “two-thirds.”
Note that the usual practice is to put a hyphen (-) between the words when you write them out:
- [latex]\dfrac{1}{2}[/latex] is usually read “one-half.”
- [latex]\dfrac{2}{2}[/latex] is read “two-halves.”
- [latex]\dfrac{3}{4}[/latex] is read as “three-quarters” or “three-fourths.”
Exercise 4
Look back again at Exercise 2 and write down the word names for your answers.
Example: [latex]\dfrac{3}{4}[/latex] = three quarters or three-fourths
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{5}{8}[/latex]
- [latex]\dfrac{2}{5}[/latex]
- [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{2}{4}[/latex]
- [latex]\dfrac{1}{3}[/latex]
Exercise 4 Answers
- Three quarters or three-fourths
- Five-eighths
- Two-fifths
- One quarter or one-fourth
- Two quarters or two-fourths
- One-third
Applying Common Fractions
We make common fractions out of many things in our lives. For example:
- I got 13 out of 15 on my English test. The score is [latex]\tfrac{13}{15}[/latex].
- The baseball pitcher struck out 2 of the 6 batters in the inning. [latex]\tfrac{2}{6}[/latex] of the batters were struck out.
- Three of the eggs in that dozen are cracked. [latex]\tfrac{3}{12}[/latex] of the eggs are cracked.
- Finish your vegetables. I gave you just 8 pieces of carrot, and you have only eaten 4 of them! [latex]\tfrac{4}{8}[/latex] of the carrots are eaten.
Exercise 5
Answer the questions using a common fraction.
Example: Jill walks for 20 minutes of the 30-minute lunch break. What fraction of her lunch break does Jill walk?
Answer: [latex]\dfrac{20}{30}[/latex]
- The test was scored out of 25. Kim got 20 marks. Write his score.
- The restaurant has 12 tables. Each waiter looks after 6 of them. What fraction of the tables does each waiter look after?
- The new litter of puppies is a big one — 10 pups. Three of the pups have floppy ears. What fraction of the puppies have floppy ears?
- Beryl planted 3 dozen tulip bulbs last fall. A mole ate one dozen of them before they flowered. That mole is in trouble!! What fraction of the tulips did the mole eat?
- Kay’s raisin cookie recipe uses 5 cups of flour altogether. Kay always puts in 2 cups of whole wheat flour and 3 cups of white flour. What fraction of the flour that she uses is whole wheat?
Exercise 5 Answers
- [latex]\dfrac{20}{30}[/latex]
- [latex]\dfrac{20}{25}[/latex]
- [latex]\dfrac{6}{12}[/latex]
- [latex]\dfrac{3}{10}[/latex]
- [latex]\dfrac{1}{3}[/latex]
- [latex]\dfrac{2}{5}[/latex]
How Do We Compare Common Fractions?
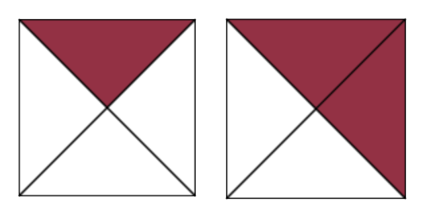
Step 1: In Figure 3.1.15, which square has more shaded parts?
The second square has more shaded parts.
Step 2: Which is larger: [latex]\dfrac{1}{4}[/latex] or [latex]\dfrac{2}{4}[/latex]?
[latex]\tfrac{2}{4}[/latex] is larger because it fills in more parts of the square.
Review:
- Greater than > Less than
- Less than < Greater than
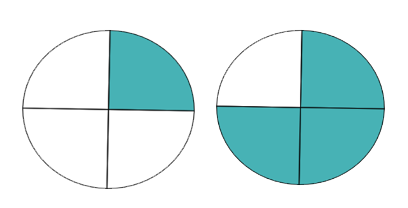
Step 1: In Figure 3.1.16, which circle is shaded more? (Hint: Look at the squares above to help answer this question.)
Step 2: Write the fractions for both drawings: [latex]\dfrac{1}{4} and \dfrac{3}{4}[/latex]
Step 3: Which fraction is larger? Place a symbol (< or >) in the space above to show your answer.
[latex]\dfrac{1}{4} < \dfrac{3}{4}[/latex]
Exercise 6
Compare fractions.
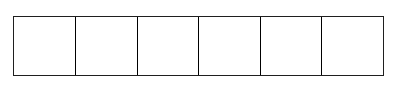

- Shade [latex]\dfrac{2}{6}[/latex] and [latex]\dfrac{5}{6}[/latex].
- Circle the fraction that is larger.
- Write a mathematical sentence stating which fraction is larger (use < or >).
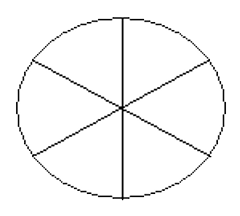

- Shade [latex]\dfrac{4}{6}[/latex] and [latex]\dfrac{3}{6}[/latex].
- Circle the fraction that is larger.
- Write a mathematical sentence stating which fraction is larger (use < or >).
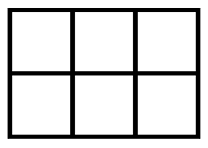

- Shade [latex]\dfrac{2}{6}[/latex] and [latex]\dfrac{1}{6}[/latex].
- Circle the fraction that is larger.
- Write a mathematical sentence stating which fraction is larger (use < or >).
Exercise 6 Answers
- [latex]\dfrac{2}{6} < \dfrac{5}{6}[/latex]
- [latex]\dfrac{4}{6} > \dfrac{3}{6}[/latex]
- [latex]\dfrac{2}{6} > \dfrac{1}{6}[/latex]
When comparing fractions:
As the numerator gets larger and the denominator stays the same, the fraction gets larger. E.g. [latex]\dfrac{3}{10} < \dfrac{7}{10}[/latex]
Exercise 7
Use the < or > symbols to show which fraction is larger.
- [latex]\dfrac{3}{4}[/latex] [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{5}{6}[/latex] [latex]\dfrac{1}{6}[/latex]
- [latex]\dfrac{9}{10}[/latex] [latex]\dfrac{1}{10}[/latex]
- [latex]\dfrac{3}{8}[/latex] [latex]\dfrac{5}{8}[/latex]
Exercise 7 Answers
- >
- >
- >
- <
Exercise 8
Show which is larger by using < or >.
- One-fourth Three-fourths
- Five-sixths Four-sixths
- Five-ninths Two-ninths
- Seven-sevenths Three-sevenths
Exercise 8 Answers
- <
- >
- >
- >
Exercise 9
Compare fractions with the same denominator. Put the fractions in order from smallest to largest.
- [latex]\dfrac{3}{4}[/latex], [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{2}{4}[/latex]
- [latex]\dfrac{6}{7}[/latex], [latex]\dfrac{2}{7}[/latex], [latex]\dfrac{3}{7}[/latex], [latex]\dfrac{1}{7}[/latex], [latex]\dfrac{5}{7}[/latex], [latex]\dfrac{4}{7}[/latex]
- [latex]\dfrac{50}{361}[/latex], [latex]\dfrac{23}{361}[/latex], [latex]\dfrac{7}{361}[/latex], [latex]\dfrac{360}{361}[/latex], [latex]\dfrac{274}{361}[/latex], [latex]\dfrac{158}{361}[/latex]
Exercise 9 Answers
-
- [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{2}{4}[/latex], [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{7}[/latex], [latex]\dfrac{2}{7}[/latex], [latex]\dfrac{3}{7}[/latex], [latex]\dfrac{4}{7}[/latex], ,
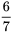
- [latex]\dfrac{7}{361}[/latex], [latex]\dfrac{23}{361}[/latex], [latex]\dfrac{50}{361}[/latex], [latex]\dfrac{158}{361}[/latex], [latex]\dfrac{274}{361}[/latex], [latex]\dfrac{360}{361}[/latex]
Using a Number Line to Compare Fractions
Using a number line is another way to look at how numbers compare to each other. Fractions can also be plotted on a number line. The number line is numbered 0 to 2. The section between 0 and 1 is split into fractions.
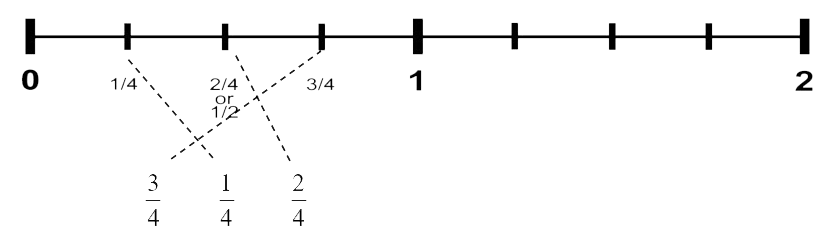
Example H
Draw a line to connect the fractions listed to the fractions on the number line (see Figure 3.1.17).
Exercise 10
Draw a line between the following fractions and the fractions on the number line.
a. [latex]\dfrac{2}{3} \; \dfrac{1}{3}[/latex]

b. [latex]\dfrac{6}{8} \; \dfrac{2}{8} \; \dfrac{5}{8} \; \dfrac{4}{8} \; \dfrac{1}{8} \; \dfrac{7}{8} \; \dfrac{3}{8}[/latex]

c. [latex]\dfrac{2}{5} \; \dfrac{1}{5}[/latex]

d. Complete the rule for comparing fractions. Circle the correct word.
As the numerator gets bigger / smaller and the denominator stays the same, the fraction gets bigger / smaller / stays the same.
Exercise 10 Answers
Check your answers for Exercise 10 with your instructor.
Exercise 11
Write the fractions on the number lines in order.
- [latex]\dfrac{1}{2} \; \dfrac{1}{4}\; \dfrac{3}{4}[/latex]

- [latex]\dfrac{2}{3}\; \dfrac{1}{3}[/latex]
- [latex]\dfrac{3}{10}\; \dfrac{7}{10}\; \dfrac{5}{10}\; \dfrac{8}{10}\; \dfrac{1}{10}[/latex]
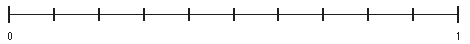
- [latex]\dfrac{5}{6}\; \dfrac{2}{6}\; \dfrac{3}{6}\; \dfrac{1}{6}[/latex]

- [latex]\dfrac{7}{12}\; \dfrac{5}{12}\; \dfrac{3}{12}\; \dfrac{10}{12}\; \dfrac{1}{12}[/latex]

Exercise 11 Answers
- [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{1}{2}[/latex], [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{3}[/latex], [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{1}{10}[/latex], [latex]\dfrac{3}{10}[/latex], [latex]\dfrac{5}{10}[/latex], [latex]\dfrac{7}{10}, \dfrac{8}{10}[/latex], [latex]\dfrac{7}{10}, \dfrac{8}{10}[/latex]
- [latex]\dfrac{1}{6}[/latex], [latex]\dfrac{2}{6}[/latex], [latex]\dfrac{3}{6}[/latex], [latex]\dfrac{5}{6}[/latex]
- [latex]\dfrac{1}{12}[/latex], [latex]\dfrac{3}{12}[/latex], [latex]\dfrac{5}{12}[/latex], [latex]\dfrac{7}{12}[/latex], [latex]\dfrac{10}{12}[/latex]
Comparing Fractions With Different Denominators
You now know how to compare fractions with the same denominator, but how do you do it when the denominators of two fractions are different?
Example I
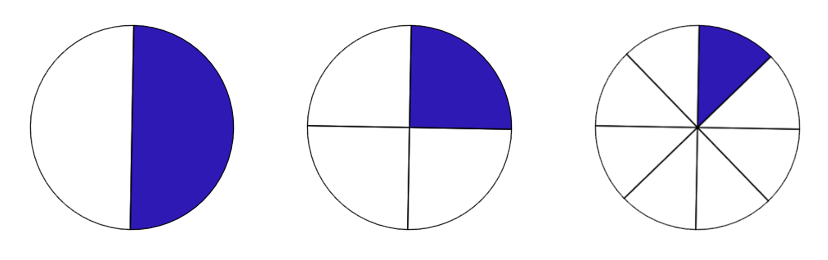
Write a fraction for each circle in Figure 3.1.18 above:
[latex]\dfrac{1}{2}[/latex], [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{1}{8}[/latex]
Which is the largest of the three fractions:
[latex]\dfrac{1}{2}[/latex]
Look at the following rectangles:
Write in the fraction for each shaded part in Figure 3.1.19:
[latex]\dfrac{1}{2}[/latex], [latex]\dfrac{1}{3}[/latex], [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{1}{5}[/latex]
Write the fractions in order from the largest to the smallest:
[latex]\dfrac{1}{5}[/latex], [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{1}{3}[/latex], [latex]\dfrac{1}{2}[/latex]
Exercise 12
Look back on the last three fraction drawing sets and compare the following fractions with < or >.
- [latex]\dfrac{1}{2}[/latex] [latex]\dfrac{1}{8}[/latex]
- [latex]\dfrac{1}{6}[/latex] [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{1}{4}[/latex] [latex]\dfrac{1}{3}[/latex]
- [latex]\dfrac{1}{3}[/latex] [latex]\dfrac{1}{8}[/latex]
Exercise 12 Answers
- >
- <
- <
- >
3.1: Practice Questions
- Write a common fraction to describe:
- the shaded part of each whole thing.
- the unshaded part of each whole thing.
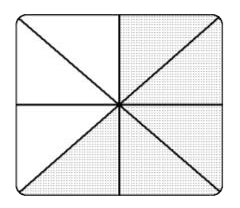
- Shaded:
- Unshaded:
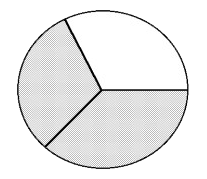
- Shaded:
- Unshaded:

- Shaded:
- Unshaded:
- Draw the following fractions.
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{5}[/latex]
- Write the word name for the following fractions.
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{5}[/latex]
- [latex]\dfrac{3}{7}[/latex]
- Answer the question using a common fraction.
- The government has ordered the closing of 24 beds at the local hospital. The townspeople are angry because the hospital only has 100 beds in all. What fraction of the hospital beds are being closed?
- The young man ordered six roses for his girlfriend. He asked for five red ones and a special yellow rose. What fraction of the roses are red?
- Compare the following fractions, use < or >.
- [latex]\dfrac{4}{5}[/latex] [latex]\dfrac{3}{5}[/latex]
- [latex]\dfrac{12}{23}[/latex] [latex]\dfrac{20}{23}[/latex]
- [latex]\dfrac{1}{3}[/latex] [latex]\dfrac{2}{3}[/latex]
3.1: Practice Answers
- Write a common fraction to describe.
-
- Square
- [latex]\dfrac{5}{8}[/latex]
- [latex]\dfrac{3}{8}[/latex]
- Circle
- [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{1}{3}[/latex]
- Rectangle
- [latex]\dfrac{7}{9}[/latex]
- [latex]\dfrac{2}{9}[/latex]
- Square
-
- Draw the following fractions.
- Write the word name for the following fractions.
- Three quarters or Three fourths
- One fifth
- Three sevenths
- Answer the question using a common fraction.
- [latex]\dfrac{24}{100}[/latex]
- [latex]\dfrac{5}{6}[/latex]
- Compare the following fractions, use < or >.
- >
- <
- <
Attribution
All figures in this chapter are from Topic A: Introducing Common Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith, via BCcampus.
This chapter has been adapted from Topic A: Introducing Common Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition (BCcampus) by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith (2023), which is under a CC BY 4.0 license.