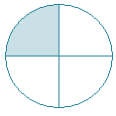
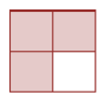
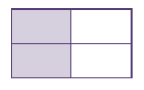
3.4: Common Fractions Review
- Write fractions from the pictures.
- Draw your own fractions.
- [latex]\dfrac{2}{5}[/latex]
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{4}{9}[/latex]
- [latex]\dfrac{1}{6}[/latex]
- [latex]\dfrac{1}{3}[/latex]
- [latex]\dfrac{7}{10}[/latex]
- Write the following fractions in words.
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{21}{25}[/latex]
- [latex]\dfrac{1}{3}[/latex]
- [latex]\dfrac{5}{6}[/latex]
- Answer the questions using a common fraction.
- Suzie jogged 20 minutes out of 1 hour. What fraction of the hour did she jog? (Remember, 1 hour = 60 minutes.)
- Oliver planted 30 garlic cloves in September. 25 shoots have come up in the spring. What fractions of garlic bulbs did not grow a shoot?
- The class usually had 8 students, but 6 did not come on Monday. What fraction of students did not come?
- Stephen made 60 Easter cookies. His brother ate 3, and his mom ate 3 more. What fraction of cookies were eaten by Stephen’s family?
- Save On Foods grocery store sold 300 dozen eggs in one week. They had 450 dozen in stock. What fraction of the stock was sold?
- The test was out of 32. Sasha got 30 marks. What was her score?
- Compare the following fractions.
- [latex]\dfrac{3}{4}[/latex] [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{9}{10}[/latex] [latex]\dfrac{3}{10}[/latex]
- [latex]\dfrac{1}{5}[/latex] [latex]\dfrac{3}{5}[/latex]
- [latex]\dfrac{3}{8}[/latex] [latex]\dfrac{7}{8}[/latex]
- seven tenths three tenths
- one quarter three quarters
- four fifths three fifths
- one twelfth eleven twelfths
- Identify each fraction by writing: proper fraction, improper fraction, or mixed number to each fraction.
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{100}{47}[/latex]
- [latex]\dfrac{5}{6}[/latex]
- [latex]\dfrac{51}{2}[/latex]
- [latex]42\dfrac{1}{4}[/latex]
- Fill in the missing parts of the chart (see Table 3.4.1).
Table 3.4.1: Question 7 Fill in the Table Improper
FractionMixed
NumberDrawing — — 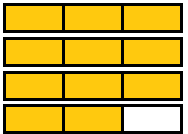
[latex]\dfrac{29}{6}[/latex] — — — [latex]2\dfrac{3}{4}[/latex] — — — 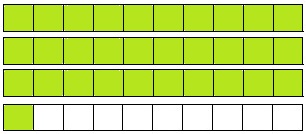
[latex]\dfrac{9}{2}[/latex] — — — [latex]3\dfrac{1}{3}[/latex] — - Convert each improper fraction to a mixed number or a whole number.
- [latex]\dfrac{9}{5}=[/latex]
- [latex]\dfrac{7}{2}=[/latex]
- [latex]\dfrac{11}{2}=[/latex]
- [latex]\dfrac{14}{5}=[/latex]
- [latex]\dfrac{4}{3}=[/latex]
- [latex]\dfrac{11}{6}=[/latex]
- [latex]\dfrac{7}{3}=[/latex]
- [latex]\dfrac{8}{4}=[/latex]
- Convert each whole number to an improper fraction. Use the denominator given to you.
- [latex]6=\dfrac{}{3}[/latex]
- [latex]5=\dfrac{}{2}[/latex]
- [latex]3=\dfrac{}{7}[/latex]
- [latex]7=\dfrac{}{3}[/latex]
- [latex]8=\dfrac{}{7}[/latex]
- [latex]1=\dfrac{}{3}[/latex]
- [latex]2=\dfrac{}{10}[/latex]
- Convert each mixed number to an improper fraction.
- [latex]6\dfrac{7}{8}=[/latex]
- [latex]2\dfrac{1}{2}=[/latex]
- [latex]15\dfrac{4}{5}=[/latex]
- [latex]20\dfrac{3}{7}=[/latex]
- [latex]18\dfrac{1}{2}=[/latex]
- [latex]5\dfrac{9}{11}=[/latex]
3.4: Review Answers
- Write fractions from the pictures.
- [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{2}{4}[/latex]
- [latex]\dfrac{4}{6}[/latex]
- [latex]\dfrac{8}{10}[/latex]
- Draw your own fractions.
- Write the following fractions in words.
- one half
- one fourth or one quarter
- three fourths or three quarters
- twenty-one twenty fifths
- one third
- five sixths
- Answer the questions using a common fraction.
- [latex]\dfrac{20}{60}[/latex]
- [latex]\dfrac{5}{30}[/latex]
- [latex]\dfrac{6}{8}[/latex]
- [latex]\dfrac{6}{60}[/latex]
- [latex]\dfrac{300}{450}[/latex]
- [latex]\dfrac{30}{32}[/latex]
- Compare the following fractions:
- >
- >
- <
- <
- >
- <
- >
- <
- Identify each fraction by writing: proper fraction, improper fraction, or mixed number to each fraction.
- proper fraction
- improper fraction
- proper fraction
- improper fraction
- mixed number
- Fill in the missing parts of the chart (see Table 3.4.2).
Table 3.4.2: Questions 7 Answers Improper
FractionMixed
NumberDrawing [latex]\dfrac{11}{3}[/latex] [latex]3\dfrac{2}{3}[/latex] 
[latex]\dfrac{29}{6}[/latex] [latex]4\dfrac{5}{6}[/latex] 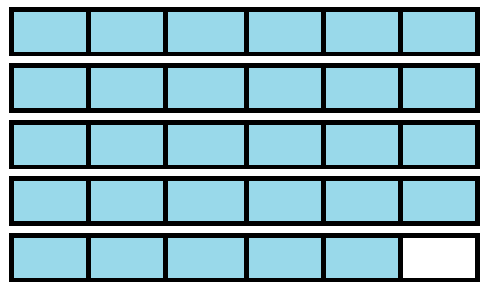
[latex]\dfrac{11}{4}[/latex] [latex]2\dfrac{3}{4}[/latex] 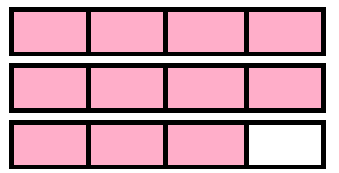
[latex]\dfrac{31}{10}[/latex] [latex]3\dfrac{1}{10}[/latex] 
[latex]\dfrac{9}{2}[/latex] [latex]4\dfrac{1}{2}[/latex] 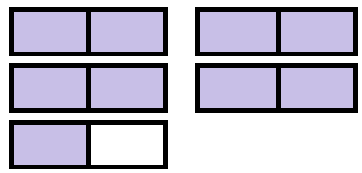
[latex]\dfrac{10}{3}[/latex] [latex]3\dfrac{1}{3}[/latex] 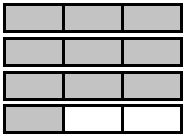
- Convert each improper fraction to a mixed number or a whole number.
- [latex]1\dfrac{4}{5}[/latex]
- [latex]3\dfrac{1}{2}[/latex]
- [latex]5\dfrac{1}{2}[/latex]
- [latex]2\dfrac{4}{5}[/latex]
- [latex]1\dfrac{1}{3}[/latex]
- [latex]1\dfrac{5}{6}[/latex]
- [latex]2\dfrac{1}{3}[/latex]
- [latex]2[/latex]
- Convert each whole number to an improper fraction. Use the denominator given to you.
- [latex]\dfrac{28}{3}[/latex]
- [latex]\dfrac{10}{2}[/latex]
- [latex]\dfrac{21}{7}[/latex]
- [latex]\dfrac{21}{3}[/latex]
- [latex]\dfrac{56}{7}[/latex]
- [latex]\dfrac{3}{3}[/latex]
- [latex]\dfrac{20}{10}[/latex]
- Convert each mixed number to an improper fraction.
- [latex]\dfrac{55}{8}[/latex]
- [latex]\dfrac{5}{2}[/latex]
- [latex]\dfrac{79}{5}[/latex]
- [latex]\dfrac{143}{7}[/latex]
- [latex]\dfrac{37}{2}[/latex]
- [latex]\dfrac{64}{11}[/latex]
Attribution
All figures in this chapter are from Unit 1 Review in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith, via BCcampus.
This chapter has been adapted from Unit 1 Review in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition (BCcampus) by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith (2023), which is under a CC BY 4.0 license.