3.5: Equivalent Fractions

Start from the left side of each drawing and shade in the fraction shown.

This shape is the whole thing:

Long rectangle. Not shaded at all

Shade [latex]\dfrac{1}{2}[/latex]:

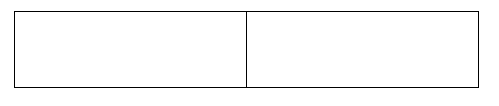Long rectangle. Divided in two segmentsShade [latex]\dfrac{2}{4}[/latex]:

Rectangle divided in four segments

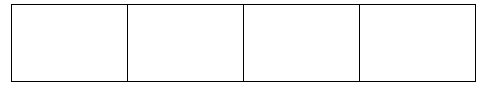
Shade [latex]\dfrac{3}{6}[/latex]:

Rectangle divided into six segements

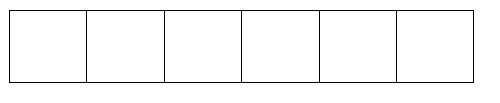
Shade [latex]\dfrac{4}{8}[/latex]:

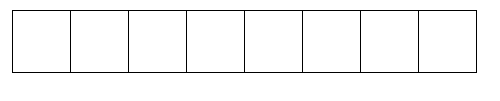
Rectangle divided into eight equal parts.

Shade [latex]\dfrac{5}{10}[/latex]:

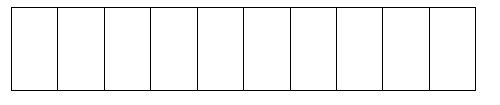
Rectangle divided into ten equal parts.

Did you notice that the amount you shaded was the same in each drawing?

The fractions that you were asked to shade are equivalent fractions. Equivalent fractions are fractions that are equal.

Now shade the fractions asked for in these drawings the same way.

This shape is the whole thing:

Long rectangle. Not shaded at all

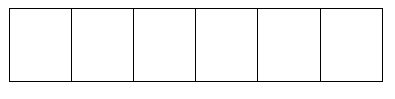
Shade [latex]\dfrac{1}{3}[/latex]:

Rectangle divided in three equal parts.

Shade [latex]\dfrac{2}{6}[/latex]

Rectangle divided into six equal parts

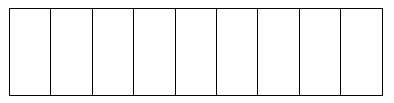
Shade [latex]\dfrac{3}{9}[/latex]:

Rectangle divided into nine equal parts.

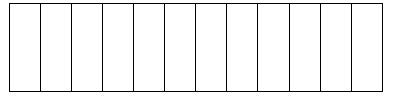
Shade [latex]\dfrac{4}{12}[/latex]:

Rectangle divided into twelve equal parts.

Shade [latex]\dfrac{5}{15}[/latex]:

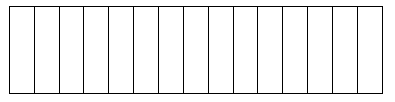
Rectangle divided into 15 equal parts.

The above examples are all equivalent fractions.

[latex]\dfrac{1}{3}[/latex] = [latex]\dfrac{2}{6}[/latex] = [latex]\dfrac{3}{9}[/latex] = [latex]\dfrac{4}{12}[/latex] = [latex]\dfrac{5}{15}[/latex]

Working with common fractions often requires using an equivalent fraction in place of the given fraction. You will learn about several processes to help you to find equivalent fractions.

Factors

Factors are the numbers which are multiplied together to make a product. An understanding of factors is needed to express fractions in the lowest terms.

Example A

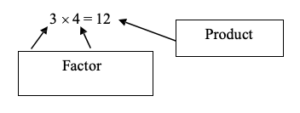
Labelled illustration. 3 x 4 and label reads Factor. Equals 12 and label reads Product.
Figure 3.5.1

We say, “The factors of 12 are 3 and 4” (see Figure 3.5.1).

Does 12 have any other factors?

What other numbers can be multiplied together to equal 12?

  • [latex]1 \times 12 = 12[/latex] or [latex]12 \times 1 = 12[/latex]
  • [latex]2 \times 6 = 12[/latex] or [latex]6 \times 2 = 12[/latex]
  • [latex]3 \times 4 = 12[/latex] or [latex]4 \times 3 = 12[/latex]

The factors of 12 are 1, 2, 3, 4, 6, 12.

Example B

Find the factors of 10.

  • [latex]1 \times 10 = 10[/latex]
  • [latex]2 \times 5 = 10[/latex]

The factors of 10 are 1, 2, 5, 10.

Example C

Find the factors of 9.

  • [latex]1 \times 9 = 9[/latex]
  • [latex]3 \times 3 = 9[/latex]

The factors of 9 are 1, 3, 9.

Exercise 1

Find all the factors.

Examples:

  • [latex]\text{The factors of 16:} \\ 1 \times 16 = 16; 2 \times 8 = 16; 4 \times 4 = 16 \\ \text{The factors of 16 are 1, 2, 4, 8, 16.}[/latex]
  • [latex]\text{The factors of 4:} \\  1 \times 4 = 4; 2 \times 2 = 4 \\  \text{The factors of 16 are 1, 2, 4, 8, 16.}[/latex]

 

  1. The factors of 8:                    
  2. The factors of 20:                    
  3. The factors of 5:                   
  4. The factors of 15:                   
  5. The factors of 21:                   
  6. The factors of 6:                   
  7. The factors of 25:                   

Exercise 1 Answers

  1. 1, 2, 4, 8
  2. 1, 2, 4, 5, 10, 20
  3. 1, 5
  4. 1, 3, 5, 15
  5. 1, 3, 7, 21
  6. 1, 2, 3, 6
  7. 1, 5, 25

Some numbers only have two factors: 1 and the number itself. These numbers are called prime numbers.

Look at Table 3.5.1 for some prime numbers.

Table 3.5.1: Factors of Prime Numbers
Prime Numbers Factors
1 1, 1
2 1, 2
3 1, 3
5 1, 5
7 1, 7
11 1, 11
13 1, 13
17 1, 17
19 1, 19
23 1, 23
29 1, 29

Add other prime numbers to the chart as you find them.

Reminder: Prime numbers only have two prime factors.

Finding Common Factors

A common factor is a number used to reduce the numerator and denominator.

Example D

What are the common factors for [latex]\dfrac{4}{6}[/latex]?

Find the factors of 4 and 6:

  • The factors of 4 are 1, 2, 4.
  • The factors of 6 are 1, 2, 3, 6.

What factors do 4 and 6 have in common?

  • 4: 1, 2, 4
  • 6: 1, 2, 3, 6

The common factors of 4 and 6 are 1 and 2.

For the above equation, the factors are 1 and 2; however, 1 is not used as a common factor. This is because 1 is a factor of all whole numbers.

Example E

What are the common factors for [latex]\dfrac{6}{15}[/latex]?

Find the factors of 6 and 15:

  • The factors of 6 are 1, 2, 3,6
  • The factors of 15 are 1, 3,5,15.

What factors do 6 and 15 have in common?

  • 6: 1, 2, 3,6
  • 15: 1, 3,5,15

The common factor of 6 and 15 is 3

Example F

Find the common factors of [latex]\dfrac{16}{24}[/latex]?

Find the factors of 16 and 24:

  • The factors of 16 are 1, 2, 4, 8, 16.
  • The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.

The common factors of 16 and 24 are: 2, 4, 8.

8 is called the greatest common factor (GCF) of 16 and 24 because it is the largest of all the common factors.

Exercise 2

Find the common factors for each set of numbers. Then, identify the greatest common factor (GCF).

Examples:

  • 10, 15
    Factors of 10: 1, 2, 5, 10
    Factors of 15: 1, 3, 5, 15
    Common factors: 5
    Greatest common factor: 5
  • 4, 16
    Factors of 4: 1, 2, 4
    Factors of 16: 1, 2, 4, 8, 16
    Common factors: 2, 4
    Greatest common factor: 4

 

  1. 9,12
    • Factors of 9:
    • Factors of 12:
    • Common factors:
    • Greatest common factor:
  2. 20, 30
    • Factors of 20:
    • Factors of 30:
    • Common factors:
    • Greatest common factor:
  3. 18, 12
    • Factors of 18:
    • Factors of 12:
    • Common factors:
    • Greatest common factor:
  4. 24, 32
    • Factors of 24:
    • Factors of 32:
    • Common factors:
    • Greatest common factor:
  5. 8, 12
    • Factors of 8:
    • Factors of 12:
    • Common factors:
    • Greatest common factor:
  6. 6, 9
    • Factors of 6:
    • Factors of 9:
    • Common factors:
    • Greatest common factor:
  7. 9,15
    • Factors of 9:
    • Factors of 15:
    • Common factors:
    • Greatest common factor:

Exercise 2 Answers

  1. 9,12
    • Factors of 9: 1, 3, 9
    • Factors of 12: 1, 2, 3, 4, 6, 12
    • Common factors: 3
    • Greatest common factor: 3
  2. 20, 30
    • Factors of 20: 1, 2, 4, 5, 10, 20
    • Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
    • Common factors: 2, 5, 10
    • Greatest common factor: 10
  3. 18, 12
    • Factors of 18: 1, 2, 3, 6, 9, 18
    • Factors of 12:, 1, 2, 3, 4, 6, 12
    • Common factors: 2, 3, 6
    • Greatest common factor: 6
  4. 24, 32
    • Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
    • Factors of 32:, 1, 2, 4, 8, 16, 32
    • Common factors: 2, 4, 8
    • Greatest common factor: 8
  5. 8, 12
    • Factors of 8: 1, 2, 4, 8
    • Factors of 12: 1, 2, 3, 4, 6, 12
    • Common factors: 2, 4
    • Greatest common factor: 4
  6. 6, 9
    • Factors of 6: 1, 2, 3, 6
    • Factors of 9: 1, 3, 9
    • Common factors: 3
    • Greatest common factor: 3
  7. 9, 15
    • Factors of 9: 1, 3, 9
    • Factors of 15: 1, 3, 5, 15
    • Common factors: 3
    • Greatest common factor: 3

Expressing Fractions in Lower Terms

Express means to say it or write it.

Lower terms mean to express equivalent fractions with smaller (lower) denominators.

The words simplify and reduce are another way to say “express fractions in lower (or lowest) terms.”

To express a fraction in the lowest terms, do this:

Step 1: Find the greatest common factor (GCF) of the numerator and denominator.

  • [latex]\dfrac{4}{12}[/latex]   The factors of 4 are 1, 2, 4
  • The factors of 12 are 1, 2, 3, 4, 6, 12

The GCF is 4.

Step 2: Divide the numerator and the denominator by the greatest common factor.

  • [latex]\dfrac{4}{12}[/latex] [latex]\dfrac{\div 4}{\div 4}[/latex]   = [latex]\dfrac{1}{3}[/latex]
  • [latex]\dfrac{4}{12}[/latex] = [latex]\dfrac{1}{3}[/latex]

Example G

[latex]\dfrac{6}{9}[/latex]

Step 1:

  • The factors of 6 are 1, 2, 3 , 6.
  • The factors of 9 are 1, 3 , 9.

The GCF is 3.

Step 2:

[latex]\dfrac{6}{9}\dfrac{\div 3}{\div 3} = \dfrac{2}{3}[/latex]

[latex]\dfrac{6}{9} = \dfrac{2}{3}[/latex]

Example H

[latex]\dfrac{15}{24}[/latex]

Step 1:

  • The factors of 15 are 1, 3,5,15
  • The factors of 24 are 1, 3, 4, 6, 8, 24.

The GCF is 3.

Step 2:

[latex]\dfrac{15}{24} \dfrac{\div 3}{\div 3} =\dfrac{5}{8}[/latex]

[latex]\dfrac{15}{24} = \dfrac{5}{8}[/latex]

There are several reasons lower terms are used:

  • The math is usually easier with lower numbers.
  • Is it easier to think of [latex]\tfrac{1}{2}[/latex] an apple or [latex]\tfrac{15}{30}[/latex] of an apple? ([latex]\tfrac{1}{2}[/latex] = [latex]\tfrac{15}{30}[/latex])
  • Do you want to think about [latex]\tfrac{155}{620}[/latex] of your pay cheque or [latex]\tfrac{1}{4}[/latex] of your pay cheque? ([latex]\tfrac{1}{4}[/latex] = [latex]\tfrac{155}{620}[/latex])
  • Always express fractions in lowest terms!

Dividing the numerator and denominator by the GCF will give an equivalent fraction in lower terms.

Exercise 3

Express each fraction in the lowest terms. (The directions could also say, “Simplify each fraction,” or, “Reduce these fractions”).

Make sure that you write in the GCF you are dividing with. Do not skip this step until you are absolutely sure you can do it correctly in your head each time.

(Good mathematicians know when to skip steps and when not to. Sometimes easy steps are never skipped by good mathematicians).

  1. [latex]\dfrac{2}{4}\dfrac{\div 2}{\div 2}= \dfrac{1}{2}[/latex],               [latex]\dfrac{3}{9}\dfrac{ \div \ \ \ }{ \div \ \ \ }[/latex] =              
  2. [latex]\dfrac{2}{12}\dfrac{\div2}{\div2}=\dfrac{1}{6}[/latex],               [latex]\dfrac{3}{15}\dfrac{ \div \ \ \ }{ \div \ \ \ }[/latex] =              
  3. [latex]\dfrac{5}{10}\dfrac{ \div \ \ }{ \div \ \ \ }[/latex] =              ,               [latex]\dfrac{4}{24}\dfrac{ \div \ \ \ }{ \div \ \ \ }[/latex] =              
  4. [latex]\dfrac{10}{25}\dfrac{ \div \ \ }{ \div\ \ \ }[/latex] =              ,               [latex]\dfrac{9}{12}\dfrac{ \div \ \ \ }{ \div \ \ \ }[/latex] =              
  5. [latex]\dfrac{3}{30}[/latex] =                       ,           [latex]\dfrac{6}{10}[/latex] =                    
  6. [latex]\dfrac{9}{24}[/latex] =                       ,           [latex]\dfrac{18}{27}[/latex] =                   
  7. [latex]\dfrac{4}{16}[/latex] =                       ,           [latex]\dfrac{3}{12}[/latex] =                   
  8. [latex]\dfrac{15}{24}[/latex] =                     ,           [latex]\dfrac{15}{25}[/latex] =                   
  9. [latex]\dfrac{2}{32}[/latex] =                       ,           [latex]\dfrac{6}{20}[/latex] =                   

Exercise 3 Answers

  1. [latex]\dfrac{1}{2}[/latex], [latex]\dfrac{1}{3}[/latex]
  2. [latex]\dfrac{1}{6}[/latex], [latex]\dfrac{1}{5}[/latex]
  3. [latex]\dfrac{1}{2}[/latex], [latex]\dfrac{1}{6}[/latex]
  4. [latex]\dfrac{2}{5}[/latex], [latex]\dfrac{3}{4}[/latex]
  5. [latex]\dfrac{1}{10}[/latex], [latex]\dfrac{3}{5}[/latex]
  6. [latex]\dfrac{3}{8}[/latex], [latex]\dfrac{2}{3}[/latex]
  7. [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{1}{4}[/latex]
  8. [latex]\dfrac{5}{8}[/latex], [latex]\dfrac{3}{8}[/latex]
  9. [latex]\dfrac{1}{16}[/latex], [latex]\dfrac{3}{10}[/latex]

Expressing Fractions in Higher Terms

Higher Terms are needed when you add and subtract fractions with different denominators.

You have learned that dividing the numerator and denominator of a fraction by a common factor gives an equivalent fraction in lower terms. You know that dividing and multiplying are opposite operations, so this next rule will match the one you just learned for reducing:

Multiplying the numerator and denominator of a fraction by the same number (a common factor) will give an equivalent fraction in higher terms.

Example I

[latex]\dfrac{3}{5}\left(\dfrac{\times 2}{\times 2}\right)=\dfrac{6}{10}[/latex]

[latex]\dfrac{3}{5}=\dfrac{6}{10}[/latex]

Example J

[latex]\dfrac{1}{2}\left(\dfrac{\times 8}{\times 8}\right)=\dfrac{8}{16}[/latex]

[latex]\dfrac{1}{2}= \dfrac{8}{16}[/latex]

Example K

[latex]\dfrac{2}{3}\left(\dfrac{\times 3}{\times 3}\right)=\dfrac{6}{9}[/latex]

[latex]\dfrac{2}{3} = \dfrac{6}{9}[/latex]

Are the Fractions Equivalent?

If the denominators are the same, you can easily judge if the fractions are equivalent by comparing the numerators.

Compare [latex]\dfrac{4}{5}[/latex] and [latex]\dfrac{3}{5}[/latex]:                    [latex]\dfrac{4}{5}[/latex] ≠ [latex]\dfrac{3}{5}[/latex] (≠ means ‘not equal’)

Compare [latex]\dfrac{12}{20}[/latex] and [latex]\dfrac{12}{20}[/latex]:                     [latex]\dfrac{12}{20} = \dfrac{12}{20}[/latex]

If the denominators are different, you might be able to rewrite one or more of the fractions so they have the same denominator.

Compare [latex]\dfrac{4}{5}[/latex] and [latex]\dfrac{6}{10}[/latex]:                     [latex]\dfrac{6}{10}\dfrac{\div 2}{\div 2}[/latex] = [latex]\dfrac{3}{5}[/latex]                    So: [latex]\dfrac{4}{5}\neq \tfrac{3}{5}[/latex]

Compare [latex]\dfrac{12}{16}[/latex] and [latex]\dfrac{5}{8}[/latex]:                    [latex]\dfrac{5}{8} \dfrac{\times 2}{\times 2}[/latex] = [latex]\dfrac{10}{16}[/latex]                    So: [latex]\dfrac{12}{16}\neq \tfrac{10}{16}[/latex]

or you could do this:            [latex]\dfrac{12}{16}[/latex][latex]\dfrac{\div 2}{\div 2}= \dfrac{6}{8}[/latex]                    So: [latex]\dfrac{6}{8}\neq\dfrac{5}{8}[/latex]

A quick method is to cross-multiply:

  1. Multiply the numerator of one fraction by the denominator of the second fraction
  2. Multiply the numerator of the other fraction by the denominator of the first fraction These are called the cross-products.
    If the cross products are the same, then the fraction is equivalent.

Example L

Compare [latex]\dfrac{4}{7}[/latex] and [latex]\dfrac{5}{9}[/latex] (see Figure 3.5.2).

A picture of two fractions and arrows between them. First fraction is numerator 4 and denominator 7. Second fraction is numberator 5 and denominator 9. Arrows direct attention from the first fraction numerator 4 to second fraction denominator 9. And from first fraction denominator 7 to second fraction numerator 5..
Figure 3.5.2

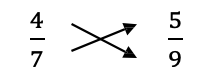
Step 1: Multiply the numerator 4 by the denominator 9.

[latex]4 \times 9 = 36[/latex]

Step 2: Multiply the denominator 7 by the numerator 5.

[latex]7 \times 5 = 35[/latex]

Step 3: The products 36 and 35 are not the same.

Therefore, [latex]\dfrac{4}{7}\neq \dfrac{5}{9}[/latex]

Example M

Compare [latex]\dfrac{2}{3}[/latex] and [latex]\dfrac{12}{18}[/latex] (see Figure 3.5.3).

 

A picture of two fractions and arrows between them. First fraction is numerator 2 and denominator 3. Second fraction is numberator 12 and denominator 18. Arrows direct attention from the first fraction numerator 2 to second fraction denominator 18. And from first fraction denominator 3 to second fraction numerator 12.
Figure 3.5.3

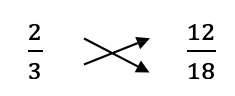
[latex]2 \times 18 = 36[/latex]

[latex]3 \times 12 = 36[/latex]

The products 36 and 36 are the same.

Therefore, [latex]\dfrac{2}{3} \neq \dfrac{12}{18}[/latex]

Example N

Compare [latex]\dfrac{24}{40}[/latex] and [latex]\dfrac{4}{10}[/latex]

[latex]24 \times 10 = 240[/latex]

[latex]40 \times 4 = 160[/latex]

The products 240 and 160 are not the same.

Therefore, [latex]\dfrac{24}{40} \neq \dfrac{4}{10}[/latex]

Exercise 4

State if each pair is equivalent (=) or not equivalent (≠). Use whichever method you wish to find the answer.

  1. [latex]\dfrac{5}{6}[/latex] =                    [latex]\dfrac{30}{60}[/latex]
  2. [latex]\dfrac{12}{24}[/latex] =                   [latex]\dfrac{1}{2}[/latex]
  3. [latex]\dfrac{6}{7}[/latex] =                     [latex]\dfrac{7}{8}[/latex]
  4. = [latex]\dfrac{2}{3}[/latex]                    [latex]\dfrac{12}{18}[/latex]
  5. [latex]\dfrac{1}{3}[/latex] =                     [latex]\dfrac{24}{72}[/latex]
  6. [latex]\dfrac{3}{4}[/latex] =                     [latex]\dfrac{15}{20}[/latex]
  7. [latex]\dfrac{12}{14}[/latex] =                     [latex]\dfrac{6}{7}[/latex]
  8. [latex]\dfrac{4}{10}[/latex] =                     [latex]\dfrac{20}{50}[/latex]
  9. [latex]\dfrac{5}{10}[/latex] =                     [latex]\dfrac{7}{14}[/latex]

Exercise 4 Answers

  1. ≠
  2. =
  3. ≠
  4. =
  5. =
  6. =
  7. =
  8. =
  9. =

Rounding Common Fractions to Whole Numbers

When rounding to a whole number, if a fraction is less than do not change the whole number.

Examples:

  • [latex]2\dfrac{4}{7}≈ 2[/latex]
  • [latex]23\dfrac{1}{3} ≈ 23[/latex]
  • [latex]\dfrac{1}{4} ≈ 0[/latex]
  • [latex]5\dfrac{3}{8}≈ 5[/latex]

If the fraction is [latex]\tfrac{1}{2}[/latex] or more, consider the fraction as another one that must be added to the whole number.

Examples:

  • [latex]2\dfrac{1}{2}[/latex] ≈ 3
  • [latex]15\dfrac{4}{5}[/latex] ≈ 16
  • [latex]6\dfrac{7}{8}[/latex] ≈ 7
  • [latex]\dfrac{3}{4}[/latex] ≈ 1

If you are not sure if a fraction is more or less than [latex]\tfrac{1}{2}[/latex], you can compare it to [latex]\tfrac{1}{2}[/latex], by making equivalent fractions with a common denominator.

Reminder: greater > smaller

Example O

Round [latex]\dfrac{2}{3}[/latex] to a whole number.

Is [latex]\dfrac{2}{3}[/latex] > [latex]\dfrac{1}{2}\text{?}\longrightarrow\dfrac{2}{3}= \dfrac{4}{6}\text{ and }\dfrac{1}{2}= \dfrac{3}{6}[/latex]

YES! [latex]\dfrac{2}{3}[/latex] > [latex]\dfrac{1}{2}\text{so}\dfrac{2}{3}≈ 1[/latex]

Example P

Round [latex]2\tfrac{4}{7}[/latex] to a whole number.

Is [latex]\dfrac{4}{7}[/latex] > [latex]\dfrac{1}{2}\text{?}\longrightarrow\dfrac{4}{7}= \dfrac{8}{14}\text{ and }\dfrac{1}{2} = \dfrac{7}{14}[/latex]

YES! [latex]\dfrac{4}{7}[/latex] > [latex]\dfrac{1}{2}[/latex] so [latex]2\dfrac{4}{7}[/latex] ≈ [latex]1[/latex]

Exercise 5

Round to the nearest whole number.

Examples:

  • [latex]\dfrac{4}{5}≈ 1[/latex]
  • [latex]2\dfrac{1}{3}≈ 2[/latex]

 

  1. [latex]18\dfrac{1}{2} ≈[/latex]                  
  2. [latex]3\dfrac{7}{8} ≈[/latex]                 
  3. [latex]9\dfrac{9}{10} ≈[/latex]                 
  4. [latex]\dfrac{1}{8} ≈[/latex]                 
  5. [latex]4\dfrac{1}{6} ≈[/latex]                 
  6. [latex]12\dfrac{7}{9} ≈[/latex]                 
  7. [latex]6\dfrac{3}{5} ≈[/latex]                 
  8. [latex]20\dfrac{3}{7} ≈[/latex]                 
  9. [latex]\dfrac{13}{15} ≈[/latex]                 
  10. [latex]99\dfrac{2}{3} ≈[/latex] 

Exercise 5 Answers

  1. 19
  2. 4
  3. 10
  4. 0
  5. 4
  6. 13
  7. 7
  8. 20
  9. 1
  10. 100

3.5:  Practice Questions

  1. Define.
      1. Equivalent                
      2. Prime number                
      3. Greatest common factor (GCF)                

     

  2. Complete the chart.
    Table 3.5.2: Question 2 Complete the Chart
    Numbers Factors Common Factors Greatest Common Factor
    12
    18    		 — — —
    15
    30    		 — — —
    7
    28    		 — — —
    6
    16    		 — — —
    18
    27    		 — — —

     

  3. Express in lowest terms.
    1. [latex]\dfrac{10}{15}[/latex] =                    .
    2. [latex]\dfrac{14}{16}[/latex] =                    .
    3. [latex]\dfrac{8}{12}[/latex] =                    .

     

  4. State if each pair of fractions is equivalent (=) or not equivalent (≠).
    1. [latex]\dfrac{5}{9}[/latex]                  [latex]\dfrac{15}{27}[/latex]
    2. [latex]\dfrac{3}{7}[/latex]                   [latex]\dfrac{15}{35}[/latex]

     

  5. Round to the nearest whole number.
    1. [latex]4\dfrac{5}{8}[/latex] ≈                      
    2. [latex]19\dfrac{4}{10}[/latex] ≈                      
    3. [latex]\dfrac{1}{2}[/latex] ≈                      
    4. [latex]6\dfrac{3}{4}[/latex] ≈                      
    5. [latex]\dfrac{1}{3}[/latex] ≈                      

3.5: Practice Answers

  1. Define.
    1. Check your definitions in the glossary
  2. Complete the chart.
    Table 3.5.3: Question 2 Answers
    Numbers Factors Common Factors Greatest Common Factor
    12
    18    		 … of 12 are 1, 2, 3, 4, 6, 12
    … of 18 are 1, 2, 3, 6, 9, 18    		 2, 3, 6 6
    15
    30    		 … of 15 are 1, 3, 5, 15

    … of 30 are 1, 2, 3, 5, 6, 10, 15, 30

    		 3, 5, 15 15
    7
    28    		 … of 7 are 1, 7
    … of 28 are 1, 2, 4, 7, 14, 28    		 7 7
    6
    16    		 … of 6 are 1, 2, 3, 6
    … of 16 are 1, 2, 4, 8, 16    		 2 2
    18
    27    		 … of 18 are 1, 2, 3, 6, 9, 18
    … of 27 are 1, 3, 9, 27    		 3, 9 9

     

  3. Express in lowest terms.
    1. [latex]\dfrac{2}{5}[/latex]
    2. [latex]\dfrac{7}{8}[/latex]
    3. [latex]\dfrac{2}{3}[/latex]

     

  4. State if each pair of fractions is equivalent (=) or not equivalent (≠).
    1. =
    2. =
    3. ≠
    4. ≠

     

  5. Round to the nearest whole number.
    1. 5
    2. 19
    3. 1
    4. 7
    5. 0

Attribution

All figures in this chapter are from Topic A: Equivalent Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith, via BCcampus.

This chapter has been adapted from Topic A: Equivalent Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition (BCcampus) by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith (2023), which is under a CC BY 4.0 license.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate PreAlgebra: Building Success Copyright © 2024 by Kim Tamblyn, TRU Open Press is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book