This is the beginning of an adventure with numbers that represent part of the whole thing. These numbers can be shown in a few different ways.

For example, 50 can be shown as a:

• Decimal fraction — 0.50
• Common fraction — [latex]\dfrac{1}{2}[/latex] or [latex]\dfrac{50}{100}[/latex]
• Percent fraction — 50%

When we talk about fractions in any of the three ways listed above, we are talking about numbers in relation to the whole thing. What do we mean by “the whole thing”? We mean one complete thing.

An example would be one full jug of juice (see Figure 4.1.1). That is 1 whole thing.

Once someone starts taking some juice, less than the whole thing remains. Now, half of the juice is gone (see Figure 4.1.2).

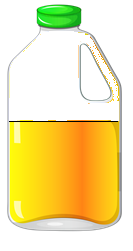
The remaining amount can be written as:

• half of one whole thing
• 0.5
• ½
• 50%

Now, almost all the juice has been taken (see Figure 4.1.3).

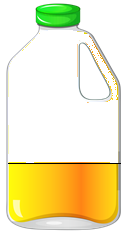
The remaining amount can be written as:

• 0.25
• ¼
• 25%

Now, there are two full jugs of juice (see Figure 4.1.4). This shows two whole things.

A fraction does not tell us much unless we know what the fraction is part of—we need to know exactly what the whole thing is! If someone says to you, “Sure, let’s go! I still have half!” you really need to know, “Half of what?”

The answer could be:

• [latex]\dfrac{1}{2}[/latex] a tank of gas.
• [latex]\dfrac{1}{2}[/latex] a paycheque.
• [latex]\dfrac{1}{2}[/latex] a vacation.
• [latex]\dfrac{1}{2}[/latex] an hour.

Fractions have meaning only when we understand the whole thing.

Decimal Fractions

Decimal fractions are one way to consider parts of the whole thing. The whole thing = 1.

You use decimal fractions every time you think about money. The dollars are written as whole numbers and the cents are written as a decimal fraction of a dollar (see Figure 4.1.5).

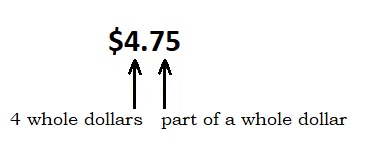
A decimal fraction has a decimal point that separates the whole number from the fraction. The decimal point looks like this:  

A whole pizza might be divided into eight pieces, ten pieces, or twelve pieces. However, for decimal fractions, the whole is always divided into ten pieces, called tenths. This is because we use a decimal system based on the number ten (“deci” is the Latin word for ten). The tenths are also divided into ten pieces to make hundredths. And then the hundredths are divided by ten to make thousandths, and so on.

Decimal fractions are often used in our daily lives, especially for money and measurement. For example:

• The total was $12.24.
• It is 3.5 kilometres from my house to the store.
• It costs $1.99 per kilogram for apples.
• She caught a 4.8-kilogram salmon.

You will be working with decimal fractions in the first two units of this book.

For example:

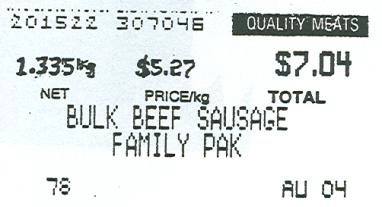
• A weight and price tag on meat packages (see Figure 4.1.6).
  

  

• The price of gas (see Figure 4.1.7).
  

  

• The price of groceries in a flyer (see Figure 4.1.8).
  

  

Common Fractions

Common fractions are a second way we will work with parts of the whole thing.

They are written with two numbers, one above the other, with a line in between. The line may be straight, or it may be on an angle.

[latex]\dfrac{1}{2}[/latex] or ¾

The numerator is the top number in a common fraction. The numerator tells how many parts. The denominator is the bottom number (see Figure 4.1.9). The denominator tells how many equal parts there are in the whole thing.

Fractions as a Percent

A third and useful way to think about parts of the whole thing is as a percent.

Percent fractions are written with a number and a percent sign.

1%         12%        50%         99%

In percent fractions, there is always a denominator of 100. That makes the arithmetic much easier and helps us to understand the fraction.

For example, if you got [latex]\tfrac{14}{20}[/latex] on a test last week and [latex]\tfrac{13}{17}[/latex] on a test this week, it is hard to get a sense of how you are doing. But if you know you got 70% last week and 76% this week, it is easier to see your improvement.

In percent fractions, the whole thing is 100%, so 100% equals 1.

Statistics and general information are often reported in percent fractions.

For example:

• Pie charts created from collected data (see Figure 4.1.7).
  

  

• Investments with your bank (see Figure 4.1.8).
  

  

• The chance of certain weather conditions occurring (see Figure 4.1.9).
  

  

What Is a Decimal Fraction?

As you know, fractions describe part of the whole thing—a fraction is smaller than 1. And as you also know, 1 (the whole thing) can be many things. For example, it can be:

• 1 dollar
• 1 city
• 1 school
• 1 pay cheque
• 1 year
• 1 second
• 1 loaf of bread
• 1 ferry ride
• etc.

A decimal might represent part of a year, part of the population of Canada, part of an hour, or part of anything.

Decimal fractions are different from common fractions in several ways:

A decimal point separates whole numbers from the fraction:

• [latex]\dfrac{1}{10} = 0.1[/latex]
• [latex]\dfrac{34}{100} = 0.34[/latex]
• [latex]\dfrac{5}{10} = 0.5[/latex]

In a decimal fraction, there is no denominator (like in Figure 4.1.20).

A whole number and a decimal can be written together. This is called a mixed decimal.

4.35        100.47          $12.39

Every whole number has a decimal point after it, even though we usually do not bother to write the decimal point unless a part of the whole (fraction) follows the whole number.

We can also put zeros to the right of the decimal point of any whole number without changing its value. Get used to thinking of a decimal point after every whole number!

• 3 = 3. = 3.0000000
• 275 = 275. = 275.0
• 100 = 100. = 100.0000000000
• $8 = $8. = $8.00

Attribution

All figures in this chapter are from Topic A: Part of the Whole Thing in Adult Literacy Fundamental Mathematics: Book 4 – 2nd Edition by Katherine Arendt, Mercedes de la Nuez, and Lix Girard, via BCcampus.

This chapter has been adapted from Topic A: Part of the Whole Thing in Adult Literacy Fundamental Mathematics: Book 4 – 2nd Edition (BCcampus) by Katherine Arendt, Mercedes de la Nuez, and Lix Girard (2023), which is under a CC BY 4.0 license.