4.10: Multiplying Decimals
Vocabulary review:
Review the diagram in Figure 4.10.1 below and try to write in the explanations of the mathematical terms. You may refer to the glossary, if you wish. For right now, it is mostly important to remember what factor means.
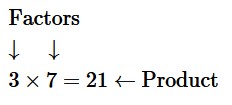
Product:
Factors:
How to Multiply Decimals
Multiplying decimals follows almost the same steps as multiplying whole numbers. This section will show you two ways to multiply decimals.
Method 1
One method is to estimate the product using whole numbers to determine where the decimal goes.
Example A
[latex]4.3 \times 5.7[/latex]
Estimate: [latex]4.3 \times 5.7 \approx 4 \times 6 = 24[/latex]
This tells us that the correct answer will be around 24 (which is two whole number places). We know that the answer will not be around 2.4 or 240.
If we take the decimals out and just multiply the digits, the answer is 2451.
[latex]\begin{array}{rr}&57\\ \times&43\\ \hline &171\\+&2280\\ \hline &2451\end{array}[/latex]
The estimate shows that the decimal point will come after two whole number places, so
[latex]4.3 \times 5.7 = 24.51[/latex].
[latex]\begin{array}{rr}&5.7\\ \times&4.3\\ \hline &171\\+&2280\\ \hline &24.51\end{array}[/latex]
Example B
[latex]23.24 \times 3.9[/latex]
Estimate: [latex]23.24 \times 3.9 \approx 23 \times 4 = 92[/latex]
The answer will be around 92. It will not be around 9.2 or 920.
If we take the decimals out and just multiply the digits, the answer is 90636.
The estimate shows that the decimal point will come after two whole number places, so
[latex]23.24\times3.9 = 90.636[/latex]
[latex]\begin{array}{rr}&23.24\\ \times &3.9\\ \hline &20916\\+&69720\\ \hline &90.636\end{array}[/latex]
If the whole numbers in the question are large, you can round to the nearest ten or hundred to help you decide where to put the decimal point. This is a quick estimate.
Example C
[latex]383.298 \times 213.87[/latex]
[latex]383.298 \times 213.87 \approx 400 \times 200 = 80\,000[/latex]
The answer will be around 80000. It will not be around 8000 or 800000.
If we take the decimals out and just multiply the digits 383.298 by 213.87, the numerals in the product are 8197594326.
The estimate shows that the whole number will go up to the ten-thousands place, which is five whole number places, so
[latex]383.298 \times 213.87 = 81\,975.94326[/latex]
Whew!
[latex]\begin{array}{rr}&383.298\\ \times &213.87\\ \hline &81975.94326\end{array}[/latex]
Exercise 1
All the multiplying has been done already. Your task is to put the decimal point in the product by doing a whole number estimate of the question.
[latex]\begin{array}{rr}&2.8\\ \times &4.3\\ \hline &84\\+&1120\\\hline&12.04\end{array}[/latex] Estimate: [latex]\begin{array}{rr}&3\\ \times &4\\ \hline &12\end{array}[/latex]
- [latex]\begin{array}[t]{rr}&56.9\\ \times&12.3\\ \hline &1707\\ &11380\\&56900\\ \hline &69987 \\ \end{array}[/latex]
- [latex]\begin{array}[t]{rr}&7.3\\ \times&19.6\\ \hline &14308 \\ \end{array}[/latex]
- [latex]\begin{array}[t]{rrrr}&28.7\\ \times&64.97\\ \hline &1864639 \\ \end{array}[/latex]
- [latex]\begin{array}[t]{rrrr}&73.2\\ \times&1.6\\ \hline &11712 \\ \end{array}[/latex]
- [latex]\begin{array}[t]{rrrr}&1.8\\ \times&1.3\\ \hline &234 \\ \end{array}[/latex]
- [latex]\begin{array}[t]{rrrr}&48.29\\ \times&55.6\\ \hline&2684924 \\ \end{array}[/latex]
- [latex]\begin{array}[t]{rrrr}&91.2\\ \times&1.5\\ \hline&13680 \\ \end{array}[/latex]
Exercise 1 Answers
- 699.87
- 143.08
- 1864.639
- 117.12
- 2.34
- 2684.924
- 136.80
Method 2
Another way of locating the decimal point in the product is to look at the number of decimal places in the decimals you are multiplying.
Example D
[latex]\begin{array}{lll}&43.23&\text{2 decimal places}\\ \times&19.6&\text{1 decimal place}\\ \hline \end{array}[/latex]
Then add the number of decimal places you counted above ([latex]2 + 1 = 3[/latex])
This is the number of decimal places you will have in your answer.
[latex]\begin{array}{lrl}&43.23&\text{2 decimal places}\\ \times&19.6&\text{1 decimal place}\\ \hline &847.\mathbf{308}&\text{3 decimal places}\end{array}[/latex]
Example E
[latex]\begin{array}{lrl}&0.35&\text{2 decimal places}\\ \times&0.47&\text{2 decimal places}\\ \hline &0.\mathbf{1645}&\text{4 decimal places}\end{array}[/latex]
Example F
[latex]\begin{array}{lrl}&13.452&\text{3 decimal places}\\ \times&30&\text{0 decimal places}\\ \hline &403.\mathbf{560}&\text{3 decimal places}\end{array}[/latex]
Exercise 2
Again, the multiplying has been done. Use the method of multiplying the understood denominators to put the decimal point in the product.
Examples:
- [latex]\begin{array}{lrl}&9.2&\text{1 decimal place}\\ \times&0.3&\text{1 decimal place}\\ \hline &2.76&\text{2 decimal places}\end{array}[/latex]
- [latex]\begin{array}{lrl}&0.27&\text{2 decimal places}\\ \times&1.8&\text{1 decimal place}\\ \hline &0.486&\text{3 decimal places}\end{array}[/latex]
- [latex]\begin{array}{rr}&6.8\\ \times&0.4\\ \hline &272 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&2.4\\ \times &0.13\\ \hline &0312 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&240\\ \times &0.05\\ \hline &1200 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.91\\ \times&6.2\\ \hline &5642 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.29\\ \times&1.2\\ \hline &0348 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.87\\ \times&0.19\\ \hline &01653 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&7.3\\ \times &3.8\\ \hline & 2744 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&4.24\\ \times &0.07\\ \hline &02968 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.042\\ \times &60\\ \hline &2520 \\ \end{array}[/latex]
Exercise 2 Answers
- 2.72
- 0.312
- 12.00
- 5.642
- 0.348
- 0.1653
- 27.74
- 0.2968
- 2.52
Exercise 3
If you had trouble with the first two exercises, then get help from your instructor. Here is extra practice if you want or need it.
Examples:
- [latex]\begin{array}{lrl}&41&\text{0 decimal places}\\ \times&0.061&\text{3 decimal places}\\ \hline &2.501&\text{3 decimal places}\end{array}[/latex]
- [latex]\begin{array}{lrl}&7.8&\text{1 decimal place}\\ \times&0.5&\text{1 decimal place}\\ \hline &3.90&\text{2 decimal places total}\end{array}[/latex]
- [latex]\begin{array}{rr}&59.275\\ \times&0.08\\ \hline &474200 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&7.18\\ \times &23.46\\ \hline &1684428 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.84\\ \times &2.1\\ \hline &1764 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&18.6\\ \times&0.3\\ \hline &558 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&100\\ \times&0.35\\ \hline &3500 \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.72\\ \times&3.4\\ \hline &2448 \\ \end{array}[/latex]
Exercise 3 Answers
- 4.74200
- 168.4428
- 1.764
- 5.58
- 35.00
- 2.448
Exercise 4
Multiply to find the product. Remember to put the decimal point in the correct place; you know two methods!
Example: [latex]\begin{array}{lr}&13.8\\ \times&3.9\\ \hline &1242\\&4140\\ \hline &53.82\end{array}[/latex]
- [latex]\begin{array}{rrr}&0.076\\ \times&24\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rrr}&2.05\\ \times &1.7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rrr}&0.429\\ \times &7.5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rrr}&96\\ \times&0.2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rrr}&1.79\\ \times&0.33\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rrr}&40.1\\ \times&0.9\\ \hline \\ \end{array}[/latex]
Exercise 4 Answers
- 1.824
- 3.485
- 3.2175
- 19.2
- 0.5907
- 36.09
Prefixing Zeros
Remember this skill?
- [latex]\dfrac{23}{1000}=0.\mathbf{0}23[/latex] — The 0 must be used after the decimal point in 0.023 to hold the tenths place. This makes it clear that the denominator is one thousand.
- [latex]\dfrac{7}{100}=0.\mathbf{0}7[/latex] — The 0 must be used after the decimal point in 0.07 to hold the tenths and hundredths place. This makes it clear that the denominator is one thousand.
- [latex]\dfrac{8}{1000}=0.\mathbf{00}8[/latex] — The 00 must be used after the decimal point in 0.008 to hold the tenths and hundredths place. This makes it clear that the denominator is one thousand.
- [latex]\dfrac{19}{10000}=0.\mathbf{00}19[/latex] — The 00 must be used after the decimal point in 0.0019 to hold the tenths and hundredths place. This makes it clear that the denominator is ten thousand.
When changing from a fraction to a decimal:
If there are not enough digits to fill all the decimal places, put zeros between the decimal point and the digits from the fraction — this is called prefixing zeros.
How does this apply to multiplying decimals? Look at the examples.
Example G
[latex]\begin{array}{lll}&0.07&\text{2 decimal places}\\ \times&0.5&\text{1 decimal place}\\ \hline &\phantom{0}35&\text{3 decimal places}\end{array}[/latex]
Uh oh! There are not enough spots in the answer to make the decimals fit in!
[latex]\begin{array}{rrc}&0.07\\ \times&0.5\\ \hline &\mathbf{00}35&\leftarrow\\&\small{3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]
Add zeros before your product. It is completely within the rules of math to do that. Then, put the decimal in the correct place.
[latex]\begin{array}{rrc}&0.07\\ \times&0.5\\ \hline &\mathbf{0.0}35&\leftarrow\\&\small{3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]
Example H
[latex]\begin{array}{lrl}&0.07&\text{2 decimal places}\\ \times&0.03&\text{+2 decimal places}\\ \hline &.\underline{\;}\,\underline{\;}75&\text{4 decimal places in product}\\&\small{4\,3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]
Example I
Look carefully at this one — it is tricky!
[latex]\begin{array}{lrl}&0.05&\text{2 decimal places}\\ \times&0.8&\text{+1 decimal place}\\ \hline &.\underline{\;}75&\text{3 decimal places in product}\\&\small{3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]
Because the last digit, the zero, is the result of multiplying 8 × 5, you must count it when working out the decimal places to put in the decimal point.
The product is forty thousandths:
[latex]\dfrac{40}{1000}=0.004[/latex]
which can now also be written as four hundredths:
[latex]\dfrac{40}{100}=0.04[/latex]
Note: If you had not counted that zero, you would have written 0.004, which is four thousandths and not correct.
Exercise 5
Find the products. Be certain to place all decimal points correctly.
Example: [latex]\begin{array}{rr}&0.35\\ \times&0.13\\ \hline&105\\&350\\ \hline & 0.0455\end{array}[/latex]
- [latex]\begin{array}{rr}&1.8\\ \times&0.05\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&300\\ \times&0.04\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&1.3\\ \times&0.027\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&500\\ \times&0.073\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.603\\ \times&0.4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&38.2\\ \times&1.9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.025\\ \times&0.25\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&3.5\\ \times&0.018\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.043\\ \times&3.3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.013\\ \times&1.4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}{rr}&0.201\\ \times&2.1\\ \hline \\ \end{array}[/latex]
Exercise 5 Answers
- 0.0455
- 0.09
- 12.00
- 0.0351
- 36.500
- 0.2412
- 72.58
- 0.00625
- 0.063
- 0.1419
- 0.0182
- 0.4221
Multiplying by 10, 100, 1000, 10000…
You can see a pattern when we multiply by a decimal number by 10, 100, 1000, 10000, and so on. Look at the following example and try to find the pattern:
- [latex]45.9264 \times 10 = 459.264[/latex]
- [latex]45.9264 \times 100 = 4592.64[/latex]
- [latex]45.9264 \times 1000 = 45926.4[/latex]
- [latex]45.9264 \times 10000 = 459264[/latex]
Do you see a pattern?
Multiply by 10
When you multiply by 10, move the decimal point one place to the right. Remember that every whole number can have a decimal point at the right.
Example J
- [latex].37 \times 10 = 3.7[/latex]
- [latex]13 \times 10 = 130.[/latex]
Exercise 6
- [latex]2.2 \times 10 =[/latex]
- [latex]6.67 \times 10 =[/latex]
- [latex]2.1 \times 100 =[/latex]
Exercise 6 Answers
- 22
- 66.7
- 210
Multiply by 100
When you multiply by 100, move the decimal point two places to the right. Note that zeros may be needed at the end of the numeral.
Example K
- [latex]4.2 \times 100 = 420.[/latex]
- [latex]6 \times 100 = 600.[/latex]
Exercise 7
- [latex]5.67 \times 100 =[/latex]
- [latex]92.737 \times 100 =[/latex]
- [latex]25 \times 100 =[/latex]
Exercise 7 Answers
- 567
- 9273.7
- 2500
Multiply by 1000
To multiply by 1000, move the decimal point three places to the right.
Example L
[latex]4.2 \times 1\,000 = 4\,200.[/latex]
Exercise 7
- [latex]6.721 \times 1\,000 =[/latex]
- [latex]1.56 \times 1\,000 =[/latex]
- [latex]0.7246 \times 1\,000 =[/latex]
- [latex]2.1 \times 1\,000 =[/latex]
Exercise 7 Answers
- 6721
- 1560
- 724.6
- 2100
Exercise 8
Write the products using the short method you now know.
- [latex]0.4 \times 10 =[/latex]
- [latex]0.27 \times 10 =[/latex]
- [latex]10 \times 0.926 =[/latex]
- [latex]10 \times 0.09 =[/latex]
- [latex]0.62 \times 100 =[/latex]
- [latex]0.119 \times 100 =[/latex]
- [latex]100 \times 2.03 =[/latex]
- [latex]100 \times 0.345 =[/latex]
- [latex]1.934 \times 1\,000 =[/latex]
- [latex]28.9 \times 100 =[/latex]
Exercise 8 Answers
- 4
- 2.7
- 9.26
- 0.9
- 62
- 11.9
- 203
- 34.5
- 1934
- 2890
Multiplying Decimals to Determine Area
The area of an object is the measurement of the amount of space the object’s surface covers. The area is described in square units.
Exercise 9
Find the area of the rectangles described below. The measures of the length (l) and width (w) have been given. You should draw and label a sketch for each.
- l = 10.5 cm
w = 6.6 cm
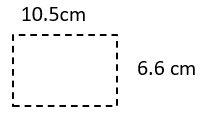
A = l × w
A = 10.5 × 6.6 cm
A = - l = 100.04 km
w = 70.2 km - l = 15.5 mm
w = 10.5 mm - l = 9.75 cm
w = 3.5 cm - l = 40.43 km
w = 10.9 km - l = 19.6 cm
w = 2.8 cm
Exercise 9 Answers
- 69.3 cm2
- 7022.808 km2
- 162.75 mm2
- 34.125 cm2
- 440.687 km2
- 54.88 cm2
Exercise 10
Find the area of each square described in the questions below. Even though this is a simple square, it is still good practice to draw a picture.
Remember: All four sides of a square are the same length.
- A square, if s = 5 cm
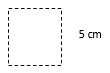
- A square, if s = 12.5 km
- A square, if s = 1.4 km
- A square, if s = 25.4 cm
Exercise 10 Answers
- 25 cm2
- 156.25 km2
- 1.96 km2
- 645.16 cm2
Word Problems Using Multiplication of Decimals
Multiplication problems usually give information about one thing and ask you to find a total amount for several of the same things. Look for this pattern in the following problems. Also, look for keywords.
Review keywords pointing to multiplication:
- product
- total
- altogether
- of
Multiplication by a decimal or fraction often uses the word “of” in word problems.
“Of” usually means multiplying one number by another number.
Example M
Kathy spends 0.25 of her salary on rent. Her salary is $1445 a month. How much is her rent?
[latex]0.25 \times $1445 = $361.25[/latex]
She spends $361.25 on rent every month.
Remember: It can be very useful to draw a picture to help yourself visualize the problem.
Exercise 11
Solve the following word problems. Estimate first.
- One crate of juice costs $11.73. How much will five crates cost?
- Estimation: $[latex]11.73 \approx $12[/latex], [latex]12 \times 5 = 60[/latex]
- Actual Solution:
- Answer:
- It takes Maria 0.75 hours to install a bathroom sink. The owner of the Ramada Hotel wants her to install 35 new sinks. How many hours of labour will Maria charge the hotel for this job?
- Estimation:
- Actual Solution:
- Answer:
- Find the longest hallway in your learning centre. Stand at one end and count how many steps you take until you reach the other end. Write that number here.
- How many steps would you take if you walked down your hallway 4.5 times?
- How many steps would you take if you walked down your hallway 33.68 times?
- Jessica’s 4×4 truck averages 15.75 kilometres per litre of gas (km/L). How far could her truck travel with 52 L of gas?
- Estimation:
- Actual Solution:
- Answer:
- The distance between Jackie’s workplace and her home is 4.3 kilometres. She walks to work in the morning and then walks back to her home at the end of the workday, five days a week. How far does she walk each week?
- Estimation:
- Actual Solution:
- Answer:
- A new subdivision is being built outside of Terrace. There are 21 new houses. Each house needs 25.2 metric tonnes of crushed rock for the driveway. How much crushed rock will be used to build all the driveways?
- Estimation:
- Actual Solution:
- Answer:
- Union workers who work on statutory holidays are paid double time and a half. This is 2.5 times their regular pay.
- The employees at the coal terminal earn $17.37 per hour. How much are they paid per hour if they work on a statutory holiday?
- Jesse worked a 7.5-hour shift at the coal terminal on Labour Day last year. What were his earnings for that day?
- Lucy’s aunt in Hartley Bay has a large 50.5 m square vegetable garden. Lucy is going to help her aunt build a barbed wire fence to keep the deer out. The fence will be made with four strands of barbed wire. How much barbed wire should Lucy buy for her aunt? The fence will look like Figure 4.10.2 below.
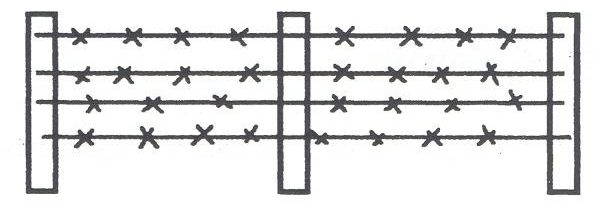
Figure 4.10.2 - Draw a picture:
- Estimation:
- Actual Solution:
- Answer:
- The directions on a bottle of carpet shampoo say one bottle will clean 50 m2 of carpet. Joyce wants to clean the wall-to-wall carpet in three rooms. The living room is 6 m by 4.5 m, the bedroom is 3 m by 4 m, and the hall is 1.2 m by 5 m. How many bottles of carpet shampoo should she buy? (This is a two-part question: Calculate the area of each of the rooms and then find the total area to be cleaned. Remember, Joyce cannot buy a partial bottle!)
- Draw a picture:
- Estimation:
- Actual Solution:
- Answer:
Exercise 11 Answers
- Estimation: [latex]$12 \times 5 \approx $60[/latex]
Actual Solution: [latex]$11.73 \times 5 = $58.65[/latex]
Five packages of juice will cost $58.65 - Estimation: [latex]1 \times 35 \approx 35 \text{ hours}[/latex]
Actual Solution: 0[latex].75 \times 35 = 26.25 \text{ hours}[/latex]
It will take Maria 26.25 hours to install the sinks. - Answers will vary. Please ask your instructor to check your work.
- Estimation: [latex]16 \text{ km } \times 50 \text{ L } \approx 800 \text{ km}[/latex]
Actual Solution: [latex]15.75 \text{ km } \times 52 \text{ L } = 819 \text{ km}[/latex]
The truck could travel 819 km. - Estimation: [latex]4 \times 10 \text{ km (5 trips there and 5 trips home) } \approx 44 \text{ seconds}[/latex]
Actual Solution: [latex]4.3 \text{ km } \times 10 = 43 \text{ km}[/latex]
Jackie walks 43 km each week. - Estimation: [latex]25 \text{ m } \times 20 \text{ m } \approx 500 \text{ m}[/latex]
Actual Solution: [latex]25.2 \text{ m } \times 21 = 529.2 \text{ m}[/latex]
There will be 529.2 metric tonnes of crushed rock used for the driveways. - Union workers:
- [latex]$17.37 \times 2.5 = $43.425 \text{ per hour}[/latex]
- [latex]$43.425 \times 7.5 \text{ hours } = $325.69[/latex]
Jesse earned $325.69 on Labour Day.
- Estimation: [latex]50 + 50 + 50 + 50 \approx 200 \text{ m }, 200 \text{ m} \times 4 \approx 800 \text{ m}[/latex]
Actual Solution: [latex]50.5 \text{ m } \times 4 = 202 \text{ m }, 202 \text{ m } \times 4 = 808 \text{ m }[/latex]
Lucy should buy 808 m of barbed wire. - Estimation:
[latex]6 \text{ m } \times 5 \text{ m } \approx 30 \text{m}^2[/latex]
[latex]3 \text{ m } \times 4 \text{ m } \approx 12 \text{m}^2[/latex]
[latex]1 \text{ m } \times 5 \text{ m } \approx 5 \text{m}^2[/latex]
[latex]30 \text{ m}^2 + 12 \text{ m}^2 + 5 \text{ m}^2 ≈ 47 \text{m}^2[/latex]
Actual Solution:
[latex]6 \text{ m } \times 4.5 \text{ m } = 27 \text{ m}^2[/latex]
[latex]3 \text{ m } \times 4 \text{ m } = 12 \text{ m}^2[/latex]
[latex]1.2 \text{ m } \times 5 \text{ m } = 6 \text{ m}^2[/latex]
[latex]27 \text{ m}^2 + 12 \text{ m}^2 + 6 \text{ m}^2 = 45 \text{ m}^2[/latex]
Joyce should buy just one bottle of carpet cleaner.
Design Your Own House Project Part 2: Roofing Your House
[May 9 – Do you want to keep this section and the one in 4.7? The unit pricing chapter, which has part 3, is not one of the chapters you wanted to include – K]
Mark: /16
Use the graph paper house sketch you made in the Design Your Own House Project Part 1 in 4.7: Subtracting Decimals to do this activity.
- What is the area of your entire house? (area = length × width) /2
- The roof of a house overhangs (sticks out past) the edges of the house by 0.5 m. Add the overhang to the length and width of your house to find the area of the roof. /2
- Before covering a roof, builders put down tarpaper, which keeps water out. Look at a hardware store flyer or go online and check prices for tar paper. /1
- Choose one type of tar paper and write down the cost per roll.
- Use your answer for question a to figure out how many rolls you will need to cover the entire roof (remember, you cannot buy part of a roll). /2
- Using your answers for questions c and d, calculate what it would cost to cover the entire roof with tar paper. /2
- Use a flyer or look at hardware stores online and choose a roofing material. /1
- Write down your choice.
- Roofing shingles are often sold in bundles that will cover 3 m2. Metal roofing materials are sold in sheets that will cover 50 square feet, which is the equivalent of 15 m2. What is the price per bundle or sheet for the material you chose in question f? /2
- Using your answer from question a, calculate how many bundles or sheets of roofing material you will need to cover your roof. /2
- Using your answers from questions g and h, calculate the total cost of roofing your house. /2
When you have finished this project, put your graph paper somewhere safe, because you will be using it again at the end of Unit 5 Topic A.
Marking Checklist for House Project Part 2
Calculations:
- The area of the house has been calculated correctly.
- The area of the roof has been calculated correctly.
- The number of rolls of tar paper has been calculated correctly.
- The cost of covering the roof in tar paper has been calculated correctly.
- The number of bundles or sheets of roofing material has been calculated correctly.
- The total cost of roofing the house has been calculated correctly.
4.10: Practice Questions
- Find the product.
- [latex]\begin{array}[t]{rr}&66\\ \times&0.7\\ \hline\\ \end{array}[/latex]
- [latex]\begin{array}[t]{rr}&7.25\\ \times&12\\ \hline\\ \end{array}[/latex]
- [latex]\begin{array}[t]{rr}&6.5\\ \times&0.6\\ \hline\\ \end{array}[/latex]
- [latex]\begin{array}[t]{rr}&19.5\\ \times&0.07\\ \hline\\ \end{array}[/latex]
- Solve the following word problem.
- Rhonda bought a 3.4 kg roast at $2.89 per kilogram. What was the cost of her roast? (Round to the nearest cent.)
- Estimation:
- Actual Solution:
- Rhonda bought a 3.4 kg roast at $2.89 per kilogram. What was the cost of her roast? (Round to the nearest cent.)
4.10: Practice Answers
-
- 46.2
- 87
- 3.9
- 1.365
- Estimate: [latex]3 \times 3 = $9[/latex]
- Actual solution: [latex]3.4 \times 2.89 = 9.826[/latex] (round to nearest cent: $9.83).
Rhonda paid $9.83 for her roast.
Attribution
All figures in this chapter are from Topic A: Multiplying Decimals in Adult Literacy Fundamental Mathematics: Book 4 – 2nd Edition by Katherine Arendt, Mercedes de la Nuez, and Lix Girard, via BCcampus.
This chapter has been adapted from Topic A: Multiplying Decimals in Adult Literacy Fundamental Mathematics: Book 4 – 2nd Edition (BCcampus) by Katherine Arendt, Mercedes de la Nuez, and Lix Girard (2023), which is under a CC BY 4.0 license.

