7.2: Solve Geometry Applications — Volume & Surface Area

In this section, we will find the volume and surface area of some three-dimensional figures. Since we will be solving applications, we will once again show our Problem-Solving Strategy for Geometry Applications.

The problem-solving strategy for geometry applications:

  1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
  2. Identify what you are looking for.
  3. Name what you are looking for. Choose a variable to represent that quantity.
  4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
  5. Solve the equation using good algebra techniques.
  6. Check the answer in the problem and make sure it makes sense.
  7. Answer the question with a complete sentence.

Find Volume & Surface Area of Rectangular Solids

A cheerleading coach wants their squad to squad paint wooden crates with the school colours to stand on at the games (see Figure 7.2.1). The amount of paint needed to cover the outside of each box is the surface area, a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure.

This wooden crate is in the shape of a rectangular solid.

 

This is an image of a wooden crate.
Figure 7.2.1

Each crate is in the shape of a rectangular solid. Its dimensions are the length, width, and height. The rectangular solid shown in Figure 7.2.2 has a length of 4 units, a width of 2 units, and a height of 3 units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.

Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. Figure 7.2.2 is a 4 by 2 by 3 rectangular solid with 24 cubic units.

 

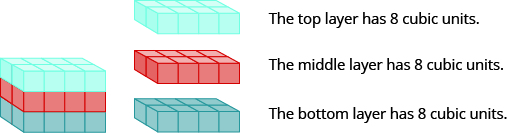
A rectangular solid is shown. Each layer is composed of 8 cubes, measuring 2 by 4. The top layer is pink. The middle layer is orange. The bottom layer is green. Beside this is an image of the top layer that says “The top layer has 8 cubic units.” The orange layer is shown and says “The middle layer has 8 cubic units.” The green layer is shown and says, “The bottom layer has 8 cubic units.”
Figure 7.2.2

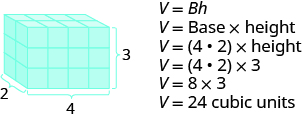
Altogether there are 24 cubic units. Notice that 24 is the [latex]\text{length}\phantom{\rule{1.0em}{0ex}}\times\phantom{\rule{1.0em}{0ex}}\text{width}\phantom{\rule{1.0em}{0ex}}\times\phantom{\rule{1.0em}{0ex}}\text{height}[/latex].

[latex]\begin{equation}\begin{split} V&=L \cdot W \cdot H \\ 24&=4 \cdot 2 \cdot 3 \end{split}\end{equation}[/latex]

The volume, V, of any rectangular solid is the product of the length, width, and height.

[latex]V=LWH[/latex]

We could also write the formula for the volume of a rectangular solid in terms of the area of the base. The area of the base, B, is equal to [latex]\text{length}\times\text{width}[/latex].

[latex]\text{B}=\text{L}\cdot\text{W}[/latex]

We can substitute B for [latex]\text{L}\cdot\text{W}[/latex] in the volume formula to get another form of the volume formula.

[latex]\begin{equation}\begin{split} V&=\mathbf{L \cdot W} \cdot H \\ V&=\mathbf{(L \cdot W)} \cdot H \\ V&=\mathbf{B}h \end{split}\end{equation}[/latex]

We now have another version of the volume formula for rectangular solids. Let’s see how this works with the [latex]4\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}2\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}3[/latex] rectangular solid we started with (see Figure 7.2.3).

 

An image of a rectangular solid is shown. It is made up of cubes. It is labeled as 2 by 4 by 3. Beside the solid is V equals Bh. Below this is V equals Base times height. Below Base is parentheses 4 times 2. The next line says V equals parentheses 4 times 2 times 3. Below that is V equals 8 times 3, then V equals 24 cubic units.
Figure 7.2.3

To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.

[latex]\begin{array}{ccccccc}{A}_{\text{front}}=L\times W\hfill & & & {A}_{\text{side}}=L\times W\hfill & & & {A}_{\text{top}}=L\times W\hfill \\ {A}_{\text{front}}=4\cdot3\hfill & & & {A}_{\text{side}}=2\cdot3\hfill & & & {A}_{\text{top}}=4\cdot2\hfill \\ {A}_{\text{front}}=12\hfill & & & {A}_{\text{side}}=6\hfill & & & {A}_{\text{top}}=8\hfill \end{array}[/latex]

Notice that for each of the three faces you see, there is an identical opposite face that does not show.

[latex]\begin{array}{l}S=\left(\text{front}+\text{back}\right)\text{+}\left(\text{left side}+\text{right side}\right)+\left(\text{top}+\text{bottom}\right)\\ S=\left(2\cdot\text{front}\right)+\left(\text{2}\cdot\text{left side}\right)+\left(\text{2}\cdot\text{top}\right)\\ S=2\cdot12+2\cdot6+2\cdot8\\ S=24+12+16\\ S=52\phantom{\rule{0.2em}{0ex}}\text{sq. units}\end{array}[/latex]

The surface area S of the rectangular solid shown in (Figure 7.2.3) is 52 square units.

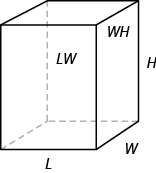
In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and width (see Figure 7.2.4). Find the area of each face you see and then multiply each area by two to account for the face on the opposite side.

[latex]S=2LH+2LW+2WH[/latex]

For each face of the rectangular solid facing you, there is another face on the opposite side. There are 6 faces in all.

 

A rectangular solid is shown. The sides are labeled L, W, and H. One face is labeled LW and another is labeled WH.
Figure 7.2.4

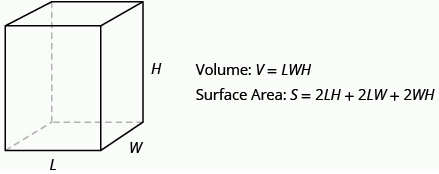
Volume and surface area of a rectangular solid:

For a rectangular solid with length L, width W, and height H:

  • Volume: [latex]V=LWH[/latex]
  • Surface Area: [latex]S=2LH+2LW+2WH[/latex]

(see Figure 7.2.5)

 

A rectangular solid is shown. The sides are labeled L, W, and H. Beside it is Volume: V equals LWH equals BH. Below that is Surface Area: S equals 2LH plus 2LW plus 2WH.
Figure 7.2.5

Example A

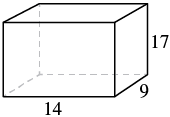
For a rectangular solid with a length of 14 cm, a height of 17 cm, and a width of 9 cm, find the a) volume and b) surface area.

Step 1 is the same for both a) and b), so we will show it just once.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.6).

 

A rectangular solid with a length of 14, width of 9, and height of 17.
Figure 7.2.6

a. Volume

Step 2: Identify what you are looking for.

The volume of the rectangular solid.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split}V&=LWH \\ V&=14 \cdot 9\cdot 17 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V=2\,142[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The volume is 2142 cubic centimetres.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the solid.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split}S&=2LH+2LW+2WH \\ S&=2(14\cdot 17)+2(14\cdot 9)+2(9\cdot 17) \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S=1\,034[/latex]

Step 6: Check. Double-check with a calculator.

Step 7: Answer the question.

The surface area is 1034 square centimetres.

Exercise 1

Find the a) volume and b) surface area of a rectangular solid with a length of 8 feet, a width of 9 feet, and a height of 11 feet.

Exercise 1 Answers

  1. 792 cu. ft
  2. 518 sq. ft

Exercise 2

Find the a) volume and b) surface area of a rectangular solid with a length of 15 feet, a width of 12 feet, and a height of 8 feet.

Exercise 2 Answers

  1. 1440 cu. ft
  2. 792 sq. ft

Example B

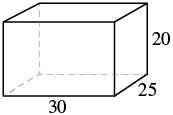
A rectangular crate has a length of 30 inches, a width of 25 inches, and a height of 20 inches. Find its a) volume and b) surface area.

Step 1 is the same for both a) and b), so we will show it just once.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.7).

 

A rectangular solid with a length of 30, width of 25, and height of 20.
Figure 7.2.7

a. Volume

Step 2: Identify what you are looking for.

The volume of the crate.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split}V&=LWH \\ V&=30 \cdot 25 \cdot 20 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V=15\,000[/latex]

Step 6: Check. Double-check your math.

Step 7: Answer the question.

The volume is 15000 cubic inches.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the crate.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split}S&=2LH+2LW+2WH \\ S&=2(30\cdot 20)+2(30\cdot 25)+2(25\cdot 20) \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S=3\,700[/latex]

Step 6: Check. Check it yourself!

Step 7: Answer the question.

The surface area is 3700 square inches.

Exercise 3

A rectangular box has a length of 9 feet, a width of 4 feet, and a height of 6 feet. Find its a) volume and b) surface area.

Exercise 3 Answers

  1. 216 cu. ft
  2. 228 sq. ft

Exercise 4

A rectangular suitcase has a length of 22 inches, a width of 14 inches, and a height of 9 inches. Find its a) volume and b) surface area.

Exercise 4 Answers

  1. 2772 cu. in.
  2. 1264 sq. in.

Volume & Surface Area of Cubes

A cube is a rectangular solid whose length, width, and height are equal. The formulas for the volume and surface area of a cube are given below. Substituting s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:

[latex]\begin{array}{ccccc}V=LWH\hfill & & & & S=2LH+2LW+2WH\hfill \\ V=\text{s}\cdot\text{s}\cdot\text{s}\hfill & & & & S=2\text{s}\cdot\text{s}+2\text{s}\cdot\text{s}+2\text{s}\cdot\text{s}\hfill \\ V={\text{s}}^{3}\hfill & & & & S=2{s}^{2}+2{s}^{2}+2{s}^{2}\hfill \\ & & & & S=6{s}^{2}\hfill \end{array}[/latex]

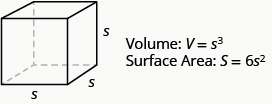
So for a cube, the formulas for volume and surface area are [latex]V={s}^{3}[/latex] and [latex]S=6{s}^{2}[/latex].

Volume and surface area of a cube:

For any cube with sides of length s:

  • Volume: [latex]V=s^3[/latex]
  • Surface Area: [latex]S=6s^2[/latex]

(see Figure 7.2.8)

 

An image of a cube is shown. Each side is labeled s. Beside this is Volume: V equals s cubed. Below that is Surface Area: S equals 6 times s squared.
Figure 7.2.8

Example C

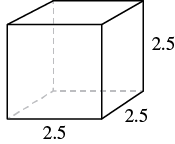
A cube is 2.5 inches on each side. Find its a) volume and b) surface area.

Step 1 is the same for both a) and b), so we will show it just once.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.9).

 

A cube with a length, width, and height of 2.5.
Figure 7.2.9

a. Volume

Step 2: Identify what you are looking for.

The volume of the cube.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split}V&=s^3 \\ V&=(2.5)^3 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V=15.625[/latex]

Step 6: Check. Check your work.

Step 7: Answer the question.

The volume is 15.625 cubic inches.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the cube.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split} S&=6s^2 \\ S&=6 \cdot (2.5)^2 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S=37.5[/latex]

Step 6: Check. The check is left to you.

Step 7: Answer the question.

The surface area is 37.5 square inches.

Exercise 5

For a cube with sides of 4.5 metres, find the a) volume and b) surface area of the cube.

Exercise 5 Answers

  1. 91.125 cu. m
  2. 121.5 sq. m

Exercise 6

For a cube with sides of 7.3 yards, find the a) volume and b) surface area of the cube.

Exercise 6 Answers

  1. 389.017 cu. yd.
  2. 319.74 sq. yd.

Example D

A notepad cube measures 2 inches on each side. Find its a) volume and b) surface area.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.10).

 

A cube with a a length, width, and height of 2
Figure 7.2.10

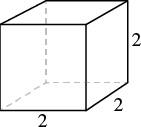
a. Volume

Step 2: Identify what you are looking for.

The volume of the cube.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split}V&=s^3 \\ V&=(2)^3 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V=8[/latex]

Step 6: Check. Check that you did the calculations correctly.

Step 7: Answer the question.

The volume is 8 cubic inches.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the cube.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute.

[latex]\begin{equation}\begin{split} S&=6s^2 \\ S&=6 \cdot (2)^2 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S=24[/latex]

Step 6: Check. The check is left to you.

Step 7: Answer the question.

The surface area is 24 square inches.

Exercise 7

A packing box is a cube measuring 4 feet on each side. Find its a) volume and b) surface area.

Exercise 7 Answers

  1. 64 cu. ft
  2. 96 sq. ft

Exercise 8

A packing box is a cube measuring 4 feet on each side. Find its a) volume and b) surface area.

Exercise 8 Answers

  1. 64 cu. ft
  2. 96 sq. ft

Find the Volume & Surface Area of Spheres

A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the centre of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.

Showing where these formulas come from, like we did for a rectangular solid, is beyond the scope of this course. We will approximate [latex]\pi[/latex] with 3.14.

Volume and surface area of a sphere:

For a sphere with radius r:

    • Volume: [latex]V=\dfrac{4}{3}\pi r^3[/latex]
    • Surface Area: [latex]S=4\pi r^2[/latex]

(see Figure 7.2.11)

 

An image of a sphere is shown. The radius is labeled r. Beside this is Volume: V equals four-thirds times pi times r cubed. Below that is Surface Area: S equals 4 times pi times r squared.
Figure 7.2.11

Example E

A sphere has a radius 6 inches. Find its a) volume and b) surface area.

Step 1 is the same for both a) and b), so we will show it just once.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.12).

 

A sphere with a radius of 6.
Figure 7.2.12

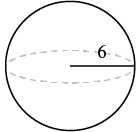
a. Volume

Step 2: Identify what you are looking for.

The volume of the sphere.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} V&= \dfrac{4}{3}\pi r^3 \\ V&\approx \dfrac{4}{3}(3.14) 6^3 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V \approx 904.32[/latex]

Step 6: Check. Double-check your math on a calculator.

Step 7: Answer the question.

The volume is approximately 904.32 cubic inches.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the sphere.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} S&= 4\pi r^2 \\ S&\approx 4(3.14)6^2 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S \approx 452.16[/latex]

Step 6: Check. Double-check your math on a calculator.

Step 7: Answer the question.

The surface area is approximately 452.16 square inches.

Exercise 9

Find the a) volume and b) surface area of a sphere with a radius of 3 centimetres.

Exercise 9 Answers

  1. 113.04 cu. cm
  2. 113.04 sq. cm

Exercise 10

Find the a) volume and b) surface area of each sphere with a radius of 1 foot.

Exercise 10 Answers

  1. 4.19 cu. ft
  2. 12.56 sq. ft

Example F

A globe of Earth is in the shape of a sphere with a radius of 14 centimetres. Find its a) volume and b) surface area. Round the answer to the nearest hundredth.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.13).

 

A globe with a radius of 14.
Figure 7.2.13

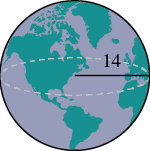
a. Volume

Step 2: Identify what you are looking for.

The volume of the sphere.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} V&= \dfrac{4}{3}\pi r^3 \\ V&\approx \dfrac{4}{3}(3.14) 14^3 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V \approx 11\,488.21[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The volume is approximately 11488.21 cubic inches.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the sphere.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} S&= 4\pi r^2 \\ S&\approx 4(3.14)14^2 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S \approx 2\,461.76[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The surface area is approximately 2461.76 square inches.

Exercise 11

A beach ball is in the shape of a sphere with a radius of 9 inches. Find its a) volume and b) surface area.

Exercise 11 Answers

  1. 3052.08 cu. in.
  2. 1017.36 sq. in.

Exercise 12

A Roman statue depicts Atlas holding a globe with a radius of 1.5 feet. Find the a) volume and b) surface area of the globe.

Exercise 12 Answers

  1. 14.13 cu. ft
  2. 28.26 sq. ft

Find the Volume & Surface Area of Cylinders

If you have ever seen a can of soda, you know what a cylinder looks like. A cylinder is a solid figure with two parallel circles of the same size at the top and bottom (see Figure 7.2.14). The top and bottom of a cylinder are called the bases. The height h of a cylinder is the distance between the two bases. For all the cylinders we will work with here, the sides and the height, h, will be perpendicular to the bases.

A cylinder has two circular bases of equal size. The height is the distance between the bases.

 

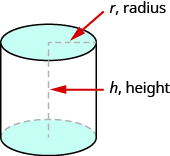
An image of a cylinder is shown. There is a red arrow pointing to the radius of the top labeling it r, radius. There is a red arrow pointing to the height of the cylinder labeling it h, height.
Figure 7.2.14

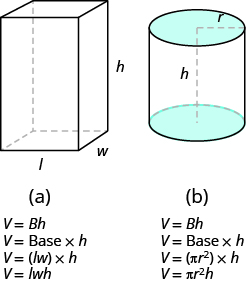
Rectangular solids and cylinders are somewhat similar because they both have two bases and a height. The formula for the volume of a rectangular solid, [latex]V=Bh[/latex], can also be used to find the volume of a cylinder.

For the rectangular solid, the area of the base, B, is the area of the rectangular base, length × width. For a cylinder, the area of the base, B, is the area of its circular base, [latex]\pi r^2[/latex] (see Figure 7.2.15) compares how the formula [latex]V=Bh[/latex] is used for rectangular solids and cylinders.

Seeing how a cylinder is similar to a rectangular solid may make it easier to understand the formula for the volume of a cylinder.

 

In (a), a rectangular solid is shown. The sides are labeled L, W, and H. Below this is V equals capital Bh, then V equals Base times h, then V equals parentheses lw times h, then V equals lwh. In (b), a cylinder is shown. The radius of the top is labeled r, the height is labeled h. Below this is V equals capital Bh, then V equals Base times h, then V equals parentheses pi r squared times h, then V equals pi times r squared times h.
Figure 7.2.15

To understand the formula for the surface area of a cylinder, think of a can of vegetables. It has three surfaces: the top, the bottom, and the piece that forms the sides of the can. If you carefully cut the label off the side of the can and unroll it, you will see that it is a rectangle (see Figure 7.2.16).

By cutting and unrolling the label of a can of vegetables, we can see that the surface of a cylinder is a rectangle. The length of the rectangle is the circumference of the cylinder’s base, and the width is the height of the cylinder.

 

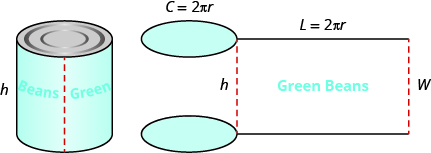
A cylindrical can of green beans is shown. The height is labeled h. Beside this are pictures of circles for the top and bottom of the can and a rectangle for the other portion of the can. Above the circles is C equals 2 times pi times r. The top of the rectangle says l equals 2 times pi times r. The left side of the rectangle is labeled h, the right side is labeled w.
Figure 7.2.16

The distance around the edge of the can is the circumference of the cylinder’s base. It is also the length L of the rectangular label. The height of the cylinder is the width W of the rectangular label. So, the area of the label can be represented as:

[latex]\begin{equation}\begin{split}A&=\textcolor{blue}{L} \cdot \textcolor{red}{W} \\ A&=\textcolor{blue}{2\pi r} \cdot \textcolor{red}{h} \end{split}\end{equation}[/latex]

To find the total surface area of the cylinder, we add the areas of the two circles to the area of the rectangle (see Figure 7.2.17).

 

A rectangle is shown with circles coming off the top and bottom.
Figure 7.2.17

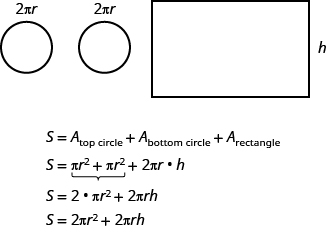
[latex]\begin{equation}\begin{split} S&={A}_{\text{top circle}}+{A}_{\text{bottom circle}}+{A}_{\text{rectangle}} \\ S&=\pi r^2 + 2\pi r \cdot h \\ S&=2\cdot \pi r^2 + 2\pi rh \\ S&=2\pi r^2 +2\pi rh \end{split}\end{equation}[/latex]

The surface area of a cylinder with radius r and height h is

[latex]S=2\pi r^2+2\pi rh[/latex]

Volume and surface area of a cylinder:

For a cylinder with radius r and height h:

  • Volume: [latex]V=\pi r^2h \text{ or } V=Bh[/latex]
  • Surface Area: [latex]S=2\pi r^2 + 2\pi rh[/latex]

(see Figure 7.2.18)

 

A cylinder is shown. The height is labeled h and the radius of the top is labeled r. Beside it is Volume: V equals pi times r squared times h or V equals capital B times h. Below this is Surface Area: S equals 2 times pi times r squared plus 2 times pi times r times h.
Figure 7.2.18

Example G

A cylinder has a height of 5 centimetres and a radius of 3 centimetres. Find the a) volume and b) surface area.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.19).

 

A cylinder with a height of 5 and a radius of 3.
Figure 7.2.19

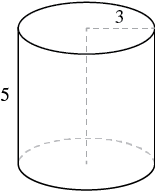
a. Volume

Step 2: Identify what you are looking for.

The volume of the cylinder.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} V&= \pi r^2 h \\ V&\approx (3.14) 3^2 \cdot 5 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V \approx 141.3[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The volume is approximately 141.3 cubic inches.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the cylinder.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} S&= 2\pi r^2 + 2\pi rh\\ S&\approx 2(3.14)3^2 + 2(3.14)(3)5\end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S \approx 150.72[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The surface area is approximately 150.72 square inches.

Exercise 13

Find the a) volume and b) surface area of a cylinder with a radius of 4 cm and a height of 7 cm.

Exercise 13 Answers

  1. 351.68 cu. cm
  2. 276.32 sq. cm

Exercise 14

Find the a) volume and b) surface area of a cylinder with a radius of 2 ft and a height of 8 ft.

Exercise 14 Answers

  1. 100.48 cu. ft
  2. 125.6 sq. ft

Example H

Find the a) volume and b) surface area of a can of soda. The radius of the base is 4 centimetres, and the height is 13 centimetres. Assume the can is shaped exactly like a cylinder.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.20).

 

A can with a height of 13 and radius of 4.
Figure 7.2.20

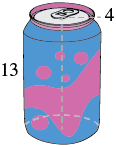
a. Volume

Step 2: Identify what you are looking for.

The volume of the cylinder.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} V&= \pi r^2 h \\ V&\approx (3.14) 4^2 \cdot 13 \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V \approx 653.12[/latex]

Step 6: Check. We leave it to you to check.

Step 7: Answer the question.

The volume is approximately 653.12 cubic centimetres.

 

b. Surface Area

Step 2: Identify what you are looking for.

The surface area of the cylinder.

Step 3: Name. Choose a variable to represent it.

Let S = surface area

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} S&= 2\pi r^2 + 2\pi rh\\ S&\approx 2(3.14)4^2 + 2(3.14)(4)13\end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]S \approx 427.04[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The surface area is approximately 427.04 square centimetres.

Exercise 15

Find the a) volume and b) surface area of a can of paint with a radius of 8 centimetres and a height of 19 centimetres. Assume the can is shaped exactly like a cylinder.

Exercise 15 Answers

  1. 3818.24 cu. cm
  2. 1356.48 sq. cm

Exercise 16

Find the a) volume and b) surface area of a cylindrical drum with a radius of 2.7 feet and a height of 4 feet. Assume the drum is shaped exactly like a cylinder.

Exercise 16 Answers

  1. 91.5624 cu. ft
  2. 113.6052 sq. ft

Find the Volume of Cones

The first image many of us have when we hear the word ‘cone’ is an ice cream cone. There are many other applications for cones (but most are not as tasty as ice cream cones). In this section, we will see how to find the volume of a cone.

In geometry, a cone is a solid figure with one circular base and a vertex. The height of a cone is the distance between its base and the vertex. The cones that we will look at in this section will always have a height perpendicular to the base (see Figure 7.2.21).

The height of a cone is the distance between its base and vertex.

 

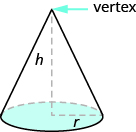
An image of a cone is shown. The top is labeled vertex. The height is labeled h. The radius of the base is labeled r.
Figure 7.2.21

Earlier in this section, we saw that the volume of a cylinder is [latex]V=\pi{r}^{2}h[/latex]. We can think of a cone as part of a cylinder. Figure 7.2.22 shows a cone placed inside a cylinder with the same height and same base. If we compare the volume of the cone and the cylinder, we can see that the volume of the cone is less than that of the cylinder.

The volume of a cone is less than the volume of a cylinder with the same base and height.

 

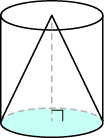
An image of a cone is shown. There is a cylinder drawn around it.
Figure 7.2.22

In fact, the volume of a cone is exactly one-third of the volume of a cylinder with the same base and height. The volume of a cone is

[latex]V=\dfrac{1}{3}Bh[/latex]

Since the base of a cone is a circle, we can substitute the formula of the area of a circle, [latex]\pi{r}^{2}[/latex], for B to get the formula for the volume of a cone.

[latex]V=\dfrac{1}{3}\pi r^2 h[/latex]

 

In this book, we will only find the volume of a cone and not its surface area.

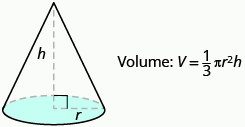
Volume of a cone:

For a cone with radius r and height h.

  • Volume: [latex]V=\dfrac{1}{3}\pi r^2 h[/latex]

(see Figure 7.2.23)

 

An image of a cone is shown. The height is labeled h, the radius of the base is labeled r. Beside this is Volume: V equals one-third times pi times r squared times h.
Figure 7.2.23

Example I

Find the volume of a cone with a height of 6 inches and a base with a radius of 2 inches.

Step 1: Read the problem. Draw the figure and label it with the given information (see Figure 7.2.24).

 

A cone with a height of 6 and radius of 2.
Figure 7.2.24

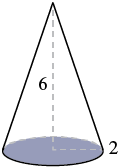
Step 2: Identify what you are looking for.

The volume of the cone.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

[latex]\begin{equation}\begin{split} V&=\dfrac{1}{3}\pi r^2 h \\V&\approx \dfrac{1}{3}(3.14)(2)^2 (6) \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V \approx 25.12[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The volume is approximately 25.12 cubic inches.

Exercise 17

Find the volume of a cone with a height of 7 inches and a radius of 3 inches.

Exercise 17 Answer

65.94 cu. in.

Exercise 18

Find the volume of a cone with a height of 9 centimetres and a radius of 5 centimetres.

Exercise 18 Answer

235.5 cu. cm

Example J

Marty’s favourite gastro pub serves french fries in a paper wrap shaped like a cone. What is the volume of a conic wrap that is 8 inches tall and 5 inches in diametre? Round the answer to the nearest hundredth.

Step 1: Read the problem. Draw the figure and label it with the given information. Notice here that the base is the circle at the top of the cone (see Figure 7.2.25).

 

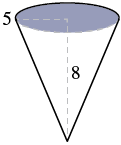
A cone with a height of 8 and radius of 5.
Figure 7.2.25

Step 2: Identify what you are looking for.

The volume of the cone.

Step 3: Name. Choose a variable to represent it.

Let V = volume

Step 4: Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex])

Notice that we were given the distance across the circle, which is its diametre. The radius is 2.5 inches.

[latex]\begin{equation}\begin{split} V&=\dfrac{1}{3}\pi r^2 h \\V&\approx \dfrac{1}{3}(3.14)(2.5)^2 (8) \end{split}\end{equation}[/latex]

Step 5: Solve the equation.

[latex]V \approx 52.33[/latex]

Step 6: Check. We leave it to you to check your calculations.

Step 7: Answer the question.

The volume of the wrap is approximately 52.33 cubic inches.

Exercise 19

How many cubic inches of candy will fit in a cone-shaped piñata that is 18 inches long and 12 inches across its base? Round the answer to the nearest hundredth.

Exercise 19 Answer

678.24 cu. in.

Exercise 20

What is the volume of a cone-shaped party hat that is 10 inches tall and 7 inches across at the base? Round the answer to the nearest hundredth.

Exercise 20 Answer

128.2 cu. in.

Additional online resources:

Key Concepts

Volume & Surface Area of a Rectangular Solid

  • [latex]V=LWH[/latex]
  • [latex]S=2LH+2LW+2WH[/latex]

Volume & Surface Area of a Cube

  • [latex]V={s}^{3}[/latex]
  • [latex]S=6{s}^{2}[/latex]

Volume & Surface Area of a Sphere

  • [latex]V=\frac{4}{3}\pi {r}^{3}[/latex]
  • [latex]S=4\pi {r}^{2}[/latex]

Volume & Surface Area of a Cylinder

  • [latex]V=\pi {r}^{2}h[/latex]
  • [latex]S=2\pi {r}^{2}+2\pi rh[/latex]

Volume of a Cone

  • For a cone with radius r and height h:
    Volume: [latex]V=\frac{1}{3}\pi {r}^{2}h[/latex]

Glossary

  • Cone — A cone is a solid figure with one circular base and a vertex.
  • Cube — A cube is a rectangular solid whose length, width, and height are equal.
  • Cylinder — A cylinder is a solid figure with two parallel circles of the same size at the top and bottom.

7.2: Practice Questions

1. Find Volume & Surface Area of Rectangular Solids

In the following exercises, find a) the volume and b) the surface area of the rectangular solid with the given dimensions.

  1. Length 2 metres, width 1.5 metres, height 3 metres
  2. Length 5 feet, width 8 feet, height 2.5 feet
  3. Length 3.5 yards, width 2.1 yards, height 2.4 yards
  4. Length 8.8 centimetres, width 6.5 centimetres, height 4.2 centimetres

In the following exercises, solve.

  1. Moving van A rectangular moving van has length 16 feet, width 8 feet, and height 8 feet. Find its a) volume and b) surface area.
  2. Gift box A rectangular gift box has length 26 inches, width 16 inches, and height 4 inches. Find its a) volume and b) surface area.
  3. Carton A rectangular carton has length 21.3 cm, width 24.2 cm, and height 6.5 cm. Find its a) volume and b) surface area.
  4. Shipping container A rectangular shipping container has length 22.8 feet, width 8.5 feet, and height 8.2 feet. Find its a) volume and b) surface area.

In the following exercises, find a) the volume and b) the surface area of the cube with the given side length.

  1. 5 centimetres
  2. 6 inches
  3. 10.4 feet
  4. 12.5 metres

In the following exercises, solve.

  1. Science center: Each side of the cube at the Discovery Science Center in Santa Ana is 64 feet long. Find its a) volume and b) surface area.
  2. Museum: A cube-shaped museum has sides 45 metres long. Find its a) volume and b) surface area.
  3. Base of a statue: The base of a statue is a cube with sides 2.8 metres long. Find its a) volume and b) surface area.
  4. Tissue box: A box of tissues is a cube with sides 4.5 inches long. Find its a) volume and b) surface area.

2. Find the Volume & Surface Area of Spheres

In the following exercises, find a) the volume and b) the surface area of the sphere with the given radius. Round answers to the nearest hundredth.

  1. 3 centimetres
  2. 9 inches
  3. 7.5 feet
  4. 2.1 yards

In the following exercises, solve. Round answers to the nearest hundredth.

  1. Exercise ball: An exercise ball has a radius of 15 inches. Find its a) volume and b) surface area.
  2. Balloon ride: The Great Park Balloon is a big orange sphere with a radius of 36 feet. Find its a) volume and b) surface area.
  3. Golf ball: A golf ball has a radius of 4.5 centimetres. Find its a) volume and b) surface area.
  4. Baseball: A baseball has a radius of 2.9 inches. Find its a) volume and b) surface area.

3. Find the Volume & Surface Area of a Cylinder

In the following exercises, find a) the volume and b) the surface area of the cylinder with the given radius and height. Round answers to the nearest hundredth.

  1. Radius 3 feet, height 9 feet
  2. Radius 5 centimetres, height 15 centimetres
  3. Radius 1.5 metres, height 4.2 metres
  4. Radius 1.3 yards, height 2.8 yards

In the following exercises, solve. Round answers to the nearest hundredth.

  1. Coffee can: A can of coffee has a radius of 5 cm and a height of 13 cm. Find its a) volume and b) surface area.
  2. Snack pack: A snack pack of cookies is shaped like a cylinder with a radius of 4 cm and a height of 3 cm. Find its a) volume and b) surface area.
  3. Barber shop pole: A cylindrical barber shop pole has a diametre of 6 inches and height of 24 inches. Find its a) volume and b) surface area.
  4. Architecture: A cylindrical column has a diametre of 8 feet and a height of 28 feet. Find its a) volume and b) surface area.

4. Find the Volume of Cones

In the following exercises, find the volume of the cone with the given dimensions. Round answers to the nearest hundredth.

  1. Height 9 feet and radius 2 feet
  2. Height 8 inches and radius 6 inches
  3. Height 12.4 centimetres and radius 5 cm
  4. Height 15.2 metres and radius 4 metres

In the following exercises, solve. Round answers to the nearest hundredth.

  1. Teepee: What is the volume of a cone-shaped teepee tent that is 10 feet tall and 10 feet across at the base?
  2. Popcorn cup: What is the volume of a cone-shaped popcorn cup that is 8 inches tall and 6 inches across at the base?
  3. Silo: What is the volume of a cone-shaped silo that is 50 feet tall and 70 feet across at the base?
  4. Sand pile: What is the volume of a cone-shaped pile of sand that is 12 metres tall and 30 metres across at the base?

5. Everyday Math

  1. Street light post: The post of a street light is shaped like a truncated cone, as shown below in Figure 7.2.26. It is a large cone minus a smaller top cone. The large cone is 30 feet tall with a base radius of 1 foot. The smaller cone is 10 feet tall with a base radius of 0.5 feet. Round to the nearest tenth.
    An image of a cone is shown. There is a dark dotted line at the top indicating a smaller cone.
    Figure 7.2.26
    1. Find the volume of the large cone.
    2. Find the volume of the small cone.
    3. Find the volume of the post by subtracting the volume of the small cone from the volume of the large cone.
  2. Ice cream cones: A regular ice cream cone is 4 inches tall and has a diametre of 2.5 inches. A waffle cone is 7 inches tall and has a diametre of 3.25 inches. Round to the nearest hundredth.
    1. Find the volume of the regular ice cream cone.
    2. Find the volume of the waffle cone.
    3. How much more ice cream fits in the waffle cone compared to the regular cone?

6. Writing Exercises

  1. The formulas for the volume of a cylinder and a cone are similar. Explain how you can remember which formula goes with which shape.
  2. Which has a larger volume, a cube of sides of 8 feet or a sphere with a diametre of 8 feet? Explain your reasoning.

7.2: Practice Answers

  1. Find volume and surface area of rectangular solids.
    1. V = 9 cu. m
      SA = 27 sq. m
    3. V = 17.64 cu. yd.
      SA = 41.58 sq. yd.
    5. V = 1024 cu. ft
      SA = 640 sq. ft
    7. V = 3350.49 cu. cm
      SA = 1,622.42 sq. cm
    9. V = 125 cu. cm
      SA = 150 sq. cm
    11. V = 1124.864 cu. ft
      SA = 648.96 sq. ft
    13. V = 262,144 cu. ft
      SA = 24,576 sq. ft
    15. V = 21.952 cu. m
      SA = 47.04 sq. m

     

  2. Find the volume and surface area of spheres.
    1. V = 113.04 cu. cm
      SA = 113.04 sq. cm
    3. V = 1766.25 cu. ft
      SA = 706.5 sq. ft
    5. V = 14130 cu. in.
      SA = 2826 sq. in.
    7. V = 381.51 cu. cm
      SA = 254.34 sq. cm

     

  3. Find the volume and surface area of a cylinder.
    1. V = 254.34 cu. ft
      SA = 226.08 sq. ft
    3. V = 29.673 cu. m
      SA = 53.694 sq. m
    5. V = 1020.5 cu. cm
      SA = 565.2 sq. cm
    7. V = 678.24 cu. in.
      SA = 508.68 sq. in.

     

  4. Find the volume of cones.
    1. 37.68 cu. ft
    3. 324.47 cu. cm
    5. 261.67 cu. ft
    7. 64108.33 cu. ft

     

  5. Everyday math.
    1. Street light post
      1. 31.4 cu. ft
      2. 2.6 cu. ft
      3. 28.8 cu. ft

     

  6. Writing exercises.
    1. Answers will vary.

References

Mathispower4u. (2011, September 2). Ex: Determine volume of a cone [Video]. YouTube. https://youtu.be/7Y0ZMnCcVGs?si=W2NB6e3r2SSZZtkh.

Attributions

All figures in this chapter are from 3.3 Solve Geometry Applications: Volume and Surface Area in Introductory Algebra by Izabela Mazur, via BCcampus.

This chapter has been adapted from 3.3 Solve Geometry Applications: Volume and Surface Area in Introductory Algebra (BCcampus) by Izabela Mazur (2021), which is under a CC BY 4.0 license.

The original chapter was adapted from 9.6 Solve Geometry Applications: Volume and Surface Area in Prealgebra 2e (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis (2020), which is under a CC BY 4.0 license. Adapted by Izabela Mazur.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate PreAlgebra: Building Success Copyright © 2024 by Kim Tamblyn, TRU Open Press is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book