4.6: Adding Decimals
Line Up the Decimals
Review place value in whole numbers and in decimal fractions.
Table 4.6.1 shows a place value chart for decimals:
| Hundreds | Tens | Ones | . | Tenths | Hundredths | Thousandths | Ten Thousandths | Hundred Thousandths |
|---|---|---|---|---|---|---|---|---|
| — | — | 3 | . | 4 | 5 | 3 | — | — |
| — | — | 0 | . | 9 | 6 | — | — | — |
Vocabulary review:
Use the example in Figure 4.6.1 below and the glossary to help you write the definitions.
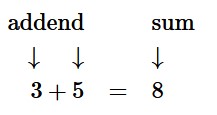
Definition of Addends:
Definition of Sum:
When adding decimals, you must be very careful to add together the digits with the same place value:
- Add thousandths to thousandths.
- Add hundredths to hundredths.
- Add tenths to tenths.
The best way to do this is to line up your decimals.
How to Add Decimals
Step 1: Write the addends underneath each other so the decimal points are in a straight column. Notice how lining up the decimals also lines up the place values.
[latex]0.43+0.2+0.804+0.1=[/latex]
Rewrite as:
[latex]\begin{array}{ll}&0.43\\&0.2\\&0.804\\+&0.1\\ \hline\end{array}[/latex]
Step 2: Put zeros at the end of the decimal fractions so that all fractions have the same number of decimal places.
[latex]\begin{array}{ll}&0.430\\&0.200\\&0.804\\+&0.100\\ \hline\end{array}[/latex]
Step 3: It may help you to put the decimal point in the answer line before you do the addition.
[latex]\begin{array}{ll}&0.430\\&0.200\\&0.804\\+&0.100\\ \hline &\phantom{0}\mathbf{.}\end{array}[/latex]
Step 4: When adding mixed decimals, be sure to keep the whole number places lined up as well. As you know, ones add to ones, tens to tens, hundreds to hundreds, and so on. Put a decimal point after any whole numbers.
[latex]62.1 + 14.58 + 6. + 7.311 + 6.23 =\ \begin{array}{lr}&62.100\\&14.580\\&6.000\\&7.311\\+&6.230 \\ \hline\end{array}[/latex]
Step 5: Add each column, starting with the decimal place farthest to the right. If the total of a column is ten or more, carry the ten number to the next column as you are used to doing with whole numbers.
[latex]\begin{array}{ll}&\small{1\; 1}\\&0.470\\&0.298\\&0.100\\+&5.600\\ \hline &6.468\end{array}[/latex]
Exercise 1
Rewrite each question in columns and add.
Examples:
- [latex]0.24 + 0.73 + 0.51 =[/latex]
[latex]\begin{array}{ll}&\scriptsize{1}\\&0.24\\&0.73\\+&0.51\\ \hline &1.48\end{array}[/latex] - [latex]0.821 + 0.14 + 0.019 =[/latex]
[latex]\begin{array}{ll}&\phantom{0.8}\scriptsize{1}\\&0.821\\&0.140\\+&0.019\\ \hline &0.980\end{array}[/latex]
- [latex]0.084 + 0.291 + 0.652 =[/latex]
- [latex]0.195 + 0.982 + 0.605 =[/latex]
- [latex]0.625 + 0.845 + 0.33 =[/latex]
- [latex]0.442 + 0.782 + 0.254 =[/latex]
Exercise 1 Answers
- 1.027
- 1.782
- 1.8
- 1.478
Exercise 2
Rewrite in columns and add.
Examples:
- [latex]1.003 + 141.2 + 0.47 =[/latex]
[latex]\begin{array}{rr}&1.003\\&141.200\\+&0.470\\ \hline &142.673\end{array}[/latex] - [latex]5.6 + 3.59 + 1\,829 =[/latex]
[latex]\begin{array}{rr}&5.60\\&3.59\\+&1829.00\\ \hline &1839.19\end{array}[/latex]
- [latex]4.6 + 2.59 + 1\,629 =[/latex]
- [latex]0.391 + 80 + 4.63 =[/latex]
- [latex]16.34 + 211.684 + 75.0697 =[/latex]
- [latex]321.6 + 485.791 + 0.001 =[/latex]
- [latex]0.22 + 46.84 + 95.6 =[/latex]
- [latex]0.042 + 0.018 + 19.1 =[/latex]
Exercise 2 Answers
- 142.673
- 1838.19
- 1636.19
- 85.021
- 303.0937
- 807.392
- 142.66
- 19.16
Exercise 3
Find the perimeter of the squares described in each question. The measure of one side has been given. Draw a picture of each square to help visualize the question.
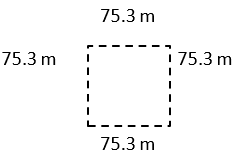
Example:
S = 75.3 m
P = S + S + S + S
P = 75.3 + 75.3 + 75.3 + 75.3 m
P = 301.2 m
- S = 12.4 mm
P = - S = 100.73 km
P = - S = 50.2 cm
- S = 16.5 m
- S = 3.25 m
Exercise 3 Answers
- 49.6 mm
- 402.92 km
- 200.8 cm
- 66 m
- 13 m
Exercise 4
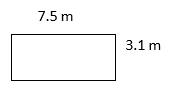
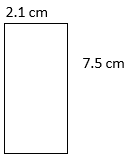
Find the perimeter of the rectangles described below. Draw your own rectangle if there is no picture.
- P = side + side + side + side
P =
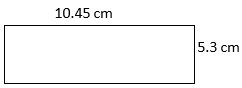
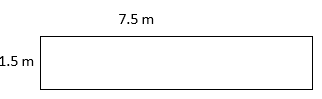
- P = side + side + side + side
P =
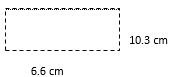
- l = 10.3 cm
w = 6.6 cm
- l = 100.03 km
w = 70.96 km - l = 9.75 cm
w = 3.5 cm
Exercise 4 Answers
- 21.2 m
- 31.5 cm
- 19.2 cm
- 18 m
- 33.8 cm
- 341.98 km
- 26.5 cm
Exercise 5
Find the perimeter of the polygons described below. Be sure the measurements are in the same unit value. Use a formula for each calculation. The formula work is started in the first two for you.
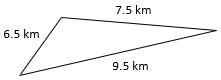
- P = Side + Side + Side
P = 6.5 km + 7.5 km + 9.5 km
P =
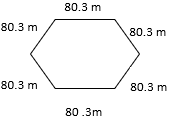
- P = Side + Side + Side + Side + Side + Side
P = + + + + +
P =
P =
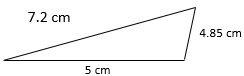
- P =
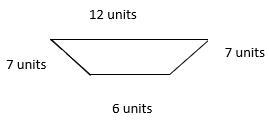
- P =
- P =

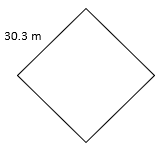
- P =
Exercise 5 Answers
- 23.5 km
- 481.8 m
- 17.05 cm
- 32 units
- 20.78 km
- 121.2 m
How to Solve Word Problems
In math, word problems describe real-life situations that involve numbers.
Often, the most difficult part of a word problem is knowing what we should do. Once we know what to do, it is much easier to figure out how to do it.
It is sort of like driving. You may be all ready to go, but before you get into the car, turn on the engine, or put your foot on the gas pedal, you need to know where you are going and figure out how to get there (see Figure 4.6.2 and 4.6.3).

The first thing to do is decide on your destination.
How do you “decide on a destination” for a math problem?
Use these steps to solve word problems:
Step 1: Question.
- Read the problem carefully.
- What is the question being asked?
- Does the problem have two parts?
- Draw a picture to help you see the problem described.
Step 2: Information.
- What information is necessary to solve the problem?
- Often, you are given extra numbers and information that are not needed.
- Keep the question (destination) in mind.
- Circle the information you need.
- Write that information on the picture you drew.
Step 3: Operation.
- Decide what arithmetic operation to use.
- Do you need to add, subtract, multiply, or divide?
- If the problem has two parts, decide what operation you need to do for each part.
- Keywords often point to the operation needed.
- Drawing a diagram or sketch is always helpful.
- Write an equation (a number sentence).
Step 4: Estimate.
- Estimate the answer to the problem.
- Round the numbers so you can work with them quickly.
- Use the operation you chose in Step 3 and come to a quick answer.
- Does this estimated answer make sense?
- Does it answer the question of the problem?
- Think carefully before you do Step 5.
Step 5: Solve.
- Solve the problem using the actual numbers.
- Check your arithmetic.
- Compare your answer in Step 4 to your estimate from Step 3.
- Think again about the question. Does your solution make sense?
- When you write your answer, include the units.
- For example: 3 dozen eggs, 7.5 kilometres, 68 people
See Table 4.6.2 for common metric units and abbreviations:
| Unit | Abbreviation |
|---|---|
| kilometre | km |
| metre | m |
| centimetre | cm |
| kilogram | kg |
| gram | g |
| litre | L |
Example A
The nutrition information on a box of cereal says that a regular serving contains 2.8 g of protein, 0.2 g of fat, 25 g of carbohydrate, and 1.9 g of “other nutrients.” Give the total number of grams in a regular serving.
Step 1: Question.
How many grams are in a regular serving?
Draw a picture (see Figure 4.6.4).

Step 2: Information.
What information is necessary to solve the problem?
- A regular serving contains 2.8 g protein, 0.2 g fat, 25 carbohydrate, and 1.9 g “other nutrients.”
- Add the information to your picture.
Step 3: Operation.
The problem lists four different amounts and asks you to find one total. “Total” is a keyword that points to addition.
Add the operation you need to your picture (see Figure 4.6.5).

Next, write an equation:
[latex]2.8 + 0.2 + 25 + 1.9 = \text{ total number of grams}[/latex]
Step 4: Estimate.
Round off each amount and add them together to get an estimated answer.
[latex]2.8 \text{ g }≈ 3 \text{ g }, 0.2 \text{ g }≈ 0 \text{ g }, 25 \text{ g }≈ 25 \text{ g }, 1.9 \text{ g }≈ 2\text{ g}[/latex]
[latex]3 \text{ g }+ 0 \text{ g }+ 25 \text{ g }+ 2 \text{ g }= 30 \text{ g}[/latex]
Does this answer make sense?
A slice of bread is about 35 grams. A serving of cereal would probably weigh a similar amount. Yes, this makes sense.
Step 5: Solve.
[latex]2.8 \text{ g }+ 0.2 \text{ g }+ 25.0 \text{ g }+ 1.9 \text{ g }= 29.9 \text{ g}[/latex]
A regular serving of cereal is 29.9 grams ← (include the units)
Check:
- Check your arithmetic.
- Compare your answer to your estimate (estimate = 30, answer =29.9).
- Does the answer make sense?
- Did you include the units in your answer?
Review keywords pointing to addition:
- sum
- plus
- total
- total amount
- altogether
- combined
- complete
- entire
- in all
- added to
- increased by
Word Problems Using Addition of Decimals
Exercise 6
Use your skills in adding decimal fractions to do the following problems. Underline keywords in the problems that will help you to recognize addition problems. Remember to draw a picture first!
Example:
A road construction crew finished surfacing 5.7 km of highway one week and 4.4 km the next week. How many kilometres did they complete in those two weeks?
- 5.7 km + 4.4 km
- Estimation: 6 km + 4 km = 10 km
- Actual Solution: [latex]\begin{array}[t]{rr}&5.7\text{ km}\\+&4.4\text{ km}\\ \hline &10.1\text{ km}\end{array}[/latex]
- Answer: The road crew completed 10.1 km of road surfacing in two weeks.
- Lisa rode her bike 4 km to her auntie’s house for a little visit. Then she rode 1.5 km to the grocery store to get apples and 0.7 km to Walmart to get bread and chips. From Walmart, she rode 3.6 km home. How far did she go on her bike altogether? (the picture has been drawn in Figure 4.6.6, but you will need to fill in the information)
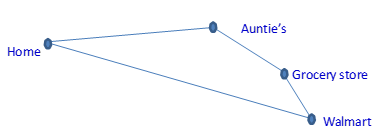
Figure 4.6.6 - Estimation:
- Actual Solution:
- Answer:
- When Crystalle bought her used car, the odometer showed 12686.4 km. In one year, she drove 13294.8 km. What did the odometer read then? (draw your own picture)
- Estimation:
- Actual Solution:
- Answer:
- A recipe for spaghetti sauce uses 1.25 kg of ground beef, 2.4 kg of fresh tomatoes, 1 kg of onions, 0.75 kg of celery, 0.5 kg of green pepper and lots of garlic and herbs. What is the total weight of the ingredients, not counting the garlic and herbs?
- Estimate:
- Actual Solution:
- Answer:
- This month, your power bill has increased by $24.67, your phone bill has an extra $13.43, and your cable bill is up $2.24. It has been an expensive month! What is the combined extra cost that you are paying this month?
- Estimate:
- Actual Solution:
- Answer:
- Wanda texted her boyfriend Curtis and asked him to pick up some groceries on the way home. He answered back, “Only have $20. Is that enough?” Wanda wanted him to buy milk ($4.86), mac and cheese ($1.99), a bag of apples ($3.99) and laundry detergent ($8.57). Does Curtis have enough money?
- Estimate:
- Actual Solution:
- Answer:
Exercise 6 Answers
- Estimation: 2 + 2 + 1 + 4 = 9
Actual Solution: 2.4 + 1.5 + 0.7 + 3.6 = 8.2
Answer: Lisa rode her bike 8.2 km altogether. - Estimation: 13000 km + 13000 km = 26000 km
Actual Solution: 12686.4 km + 13294.8 km = 25981.2 km
Answer: The odometer read 25 981.2 km after one year. - Estimation: 1 kg + 2 kg + 1 kg + 1 kg + 1 kg = 6 kg
Actual Solution: 1.25 kg + 2.4 kg + 1 kg + 0.75 kg + 0.5 kg = 5.9 kg
Answer: The total weight of the ingredients is 5.9 kg. - Estimation: $25 + $13 + $2 = $40
Actual solution: $24.67 + $13.43 + $2.24 = $40.34
Answer: The extra cost you are paying is $40.34. - Estimation: $5 + $2 + $4 + 9 = $20
Actual solution: $4.86 + $1.99 + $3.99 + $8.57 = $19.41
Answer: The groceries will cost $19.41 so yes, Curtis has enough money.
4.6: Practice Questions
- Find the sum.
- [latex]\begin{array}{rr}&3.67\\&12.55\\&8.19\\+&5.67\\ \hline\\ \end{array}[/latex]
- [latex]5.27+2.4+8+6.93+10.27=[/latex]
- [latex]\begin{array}{rr}&4.648\\&1.92\phantom{0}\\&1.275\\+&86.9\phantom{00}\\ \hline\\ \end{array}[/latex]
- [latex]2.72+0.6+110+17/223=[/latex]
- Solve the following word problem.
- Gwen mailed Christmas presents to her family. She sent a 3.7 kg box to her daughter in Vancouver, a 2.145 kg package to her sister’s family in Campbell River, a box to Prince George that was 1.06 kg, and a parcel to Kitwanga that was 4 kg. What was the combined weight of Gwen’s parcels?
- Estimate:
- Actual Solution:
- Answer:
- Gwen mailed Christmas presents to her family. She sent a 3.7 kg box to her daughter in Vancouver, a 2.145 kg package to her sister’s family in Campbell River, a box to Prince George that was 1.06 kg, and a parcel to Kitwanga that was 4 kg. What was the combined weight of Gwen’s parcels?
4.6: Practice Answers
- Find the sum.
- 30.08
- 32.87
- 94.743
- 130.543
- Solve the following word problem.
- Estimation: 4 kg + 2 kg +1 kg + 4 kg = 11 kg
- Actual Solution: 3.7 kg + 2.145 kg + 1.06 kg + 4 kg = 10.905 kg
- Answer: The combined weight of the parcels was 10.905 kg.
Attribution
All figures in this chapter are from Topic A: Adding Decimals in Adult Literacy Fundamental Mathematics: Book 4 – 2nd Edition by Katherine Arendt, Mercedes de la Nuez, and Lix Girard, via BCcampus.
This chapter has been adapted from Topic A: Adding Decimals in Adult Literacy Fundamental Mathematics: Book 4 – 2nd Edition (BCcampus) by Katherine Arendt, Mercedes de la Nuez, and Lix Girard (2023), which is under a CC BY 4.0 license.

