3.2: Common Fractions

There are three types of fractions:

  • Proper fractions are part of the whole thing.
  • Improper fractions are equal to 1 or are greater than 1.
  • Mixed numbers are greater than one.

In a proper fraction, the numerator is smaller than the denominator. Proper fractions are less than one.

  • [latex]\dfrac{3}{4}<1[/latex]
  • [latex]\dfrac{2}{5}<1[/latex]
  • [latex]\dfrac{9}{10}<1[/latex]
  • [latex]\dfrac{4}{7}<1[/latex]

In improper fractions, the numerator is the same or larger than the denominator.

  • [latex]\dfrac{4}{4}=1[/latex]
  • [latex]\dfrac{3}{3}=1[/latex]
  • [latex]\dfrac{8}{3}>1[/latex]
  • [latex]\dfrac{9}{7}>1[/latex]

In mixed numbers, a whole number and a proper fraction are used together.

  • [latex]1\dfrac{1}{2}>1[/latex]
  • [latex]4\dfrac{3}{7}>1[/latex]
  • [latex]3\dfrac{2}{5}>1[/latex]
  • [latex]1\dfrac{9}{10}>1[/latex]

Here are some pictures to visualize mixed numbers:

Example A

Three apple halves.
Figure 3.2.1

You want to give three small children only [latex]\dfrac{1}{2}[/latex] an apple each. You need three half apples (see Figure 3.2.1).

You can write that as [latex]\dfrac{3}{2}[/latex] (three halves). How will you get [latex]\dfrac{3}{2}[/latex] of an apple?

You must use more than one apple.

[latex]\dfrac{3}{2} = 1\dfrac{1}{2} \text{ apples}[/latex]

This is one whole apple and [latex]\dfrac{1}{2}[/latex] of another one.

Example B

10 slices of pizza. One whole pizza with eight slices and two additional slices from another pizza.
Figure 3.2.2

In Figure 3.2.2, 10 pieces of pizza are shown. Each pizza was cut into 8 pieces.

The fraction can be written as [latex]\dfrac{10}{8}[/latex], which is an improper fraction.

It can also be written as a mixed number: [latex]1\dfrac{2}{8}[/latex]. This is 1 whole pizza and [latex]\dfrac{2}{8}[/latex] of another one.

Exercise 1

Answer these questions.

  1. Two apples cut into quarters. There are seven pieces of apple left.
    Figure 3.2.3
    1. How many pieces of apple are shown in Figure 3.2.3?
    2. Each apple was cut into 4 pieces, so the denominator is .
    3. Write the improper fraction that describes the photo.
    4. The photo shows whole apple and of a second apple.
    5. Write the mixed number that describes the apple.
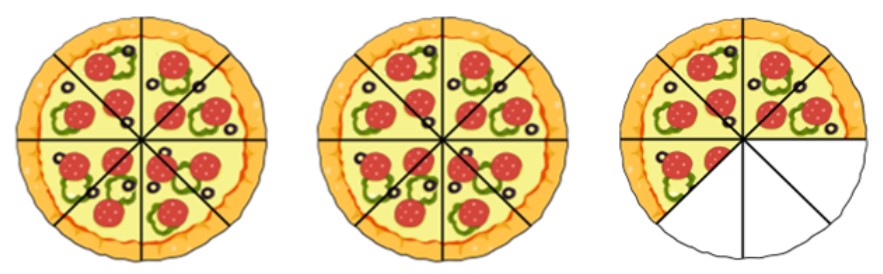
  2. Three pizzas cut into 8 pieces. There are two whole pizzas. The third pizza has 5 slices left.
    Figure 3.2.4
    1. How many pieces of pizza are shown in Figure 3.2.4?
    2. Each pizza was cut into 8 pieces, so the denominator is .
    3. Write the improper fraction that describes the photo.
    4. The photo shows whole pizzas and of a third pizza.
    5. Write the mixed number that describes the pizza.

Exercise 1 Answers

  1. Apples.
    1. [latex]7[/latex]
    2. [latex]4[/latex]
    3. [latex]\dfrac{7}{4}[/latex]
    4. [latex]1\text{ and }\dfrac{3}{4}[/latex]
    5. [latex]1\dfrac{3}{4}[/latex]
  2. Pizza.
    1. [latex]21[/latex]
    2. [latex]8[/latex]
    3. [latex]\dfrac{21}{8}[/latex]
    4. [latex]2\text{ and }\dfrac{5}{8}[/latex]
    5. [latex]2\dfrac{5}{8}[/latex]

Exercise 2

Write the improper fraction and the mixed number that describe the shaded part in each drawing.

First, decide on the denominator. The denominator is what one whole thing has been divided into.

Example:

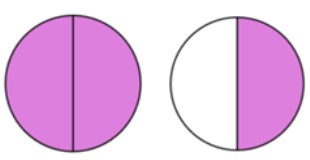Two circles divided in half. One circle is entirely shaded in. The other circle only has one half shaded in.Answer: [latex]\dfrac{3}{2}=1\dfrac{1}{2}[/latex]

  1. Four shapes divided into eight. Three shapes are all shaded in. One shape has three sections shaded.
  2. 6 rectangles divided into 6. 5 rectanges are all shaded in. One rectangle has two section shaded in.
  3. 2 shapes divided into 9 sections. One shape is all shaded in. The other shape has 5 sections shaded in.
  4. 3 squares divided into 4. Two squares are all shaded in. One square has three sections shaded in.

Exercise 2 Answers

  1. [latex]\dfrac{27}{8} = 3\dfrac{3}{8}[/latex]
  2. [latex]\dfrac{32}{6} = 5\dfrac{2}{6}[/latex]
  3. [latex]\dfrac{14}{9} = 1\dfrac{5}{9}[/latex]
  4. [latex]\dfrac{11}{4} = 2\dfrac{3}{4}[/latex]

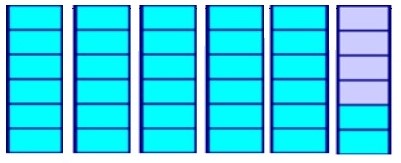
Now, it is your turn to draw some mixed numbers. The following is an example of how to do that.

Example C

Shade in this fraction: [latex]4\dfrac{3}{4}[/latex]

(Note: you will not need to use all the squares drawn below.)

Answer: see Figure 3.2.5.

 

Six squares divided into 4 sections. Four squares are all shaded in. One square has three sections shaded in. The last square is not shaded in.
Figure 3.2.5

Exercise 3

Shade the following mixed fractions in the given shapes.

  1. [latex]2\dfrac{3}{5}\hspace{1cm}[/latex]
    Four rectangles, each divided into five sections.
  2. [latex]3\dfrac{2}{3}\hspace{1cm}[/latex]
    Five circles each divided into thirds.
  3. [latex]5\dfrac{1}{4}\hspace{1cm}[/latex]
    9 rectangles each divided into four sections.
  4. [latex]1\dfrac{1}{2}\hspace{1cm}[/latex]
    Four rectangles each divided in half.

Draw the following mixed fractions:

  1. [latex]4\dfrac{1}{2}[/latex]
  2. [latex]3\dfrac{4}{5}[/latex]
  3. [latex]2\dfrac{2}{3}[/latex]
  4. [latex]5\dfrac{3}{4}[/latex]

Exercise 3 Answers

  1. 5 rectangles divided into 5 sections. 2 are fully shaded. One has three sections shaded. Two are not shaded.
  2. 5 circles divided into 3 sections. 3 are fully shaded. 1 has 2 sections shaded. 2 are not shaded.
  3. 9 rectangles divided into 4 sections. 5 are fully shaded. 1 has 1 section shaded. 3 are not shaded.
  4. 4 rectangles divided into 2 sections. 1 is fully shaded. 1 has 1 section shaded. 2 are not shaded.
  5. 5 circles divided into 2 sections. 4 are fully shaded. 1 has 1 section shaded.
  6. 5 rectangles divided into 5 sections. 3 are fully shaded. 1 has 4 sections shaded. 1 is not shaded.
  7. 3 circles divided into 3 sections. 2 are fully shaded. 1 has 2 sections shaded.
  8. 6 rectangles divided into 4 sections. 5 are fully shaded. 1 has 3 sections shaded.

Writing Improper Fractions as Mixed Numbers

In the last exercise, you were able to write (rename) an improper fraction as a mixed number by looking at the drawing — you could see how many whole things were represented.

You could see that:

  • If the denominator was 3 — Every time you had [latex]\tfrac{3}{3}[/latex] A circle split into three equal segments. All segments are shaded green.that was one whole.
  • If the denominator was 6 — Every time you had [latex]\tfrac{6}{6}[/latex] A rectangle split into six equal segments. All segments are shaded grey.that was one whole
  • And so on.

An improper fraction is written (renamed) as a mixed number by dividing the numerator by the number of parts in the whole (the denominator).

Example D

Write [latex]\dfrac{8}{5}[/latex] as a mixed number.

Step 1: Write as a long division problem or as a short division question.

[latex]\require{enclose}\text{denominator}\enclose{longdiv}{\text{numerator}}=5\enclose{longdiv}{8}[/latex]

[latex]\text{numerator}\div\text{denominator} = 8\div5[/latex]

Step 2: Divide. Write the remainder as a fraction, using the same denominator.

  1. The 1 becomes the whole number.
  2. Use the remainder (3) as the numerator
  3. Use the divisor (5) as the denominator.

[latex]\begin{array}{r}1\\ 5\enclose{longdiv}{8}\\-5\\ \hline\text{R }3\end{array}[/latex]               or              [latex]8\div5=1\text{ R }3[/latex]

[latex]\dfrac{8}{5}=1\dfrac{3}{5}[/latex]

Example E

Write [latex]\dfrac{16}{4}[/latex] as a mixed number.

[latex]4\enclose{longdiv}{16}[/latex] or [latex]16\div4[/latex]

[latex]\begin{array}{r}4\\ 4\enclose{longdiv}{16}\\-16\\ \hline0\end{array}[/latex]              or              [latex]16\div4=4[/latex]

[latex]\dfrac{16}{4}=4[/latex]

Exercise 4

Rewrite each improper fraction as an equivalent mixed number or whole number.

  1. [latex]\dfrac{9}{2}=[/latex]
  2. [latex]\dfrac{11}{10}=[/latex]
  3. [latex]\dfrac{20}{4}=[/latex]
  4. [latex]\dfrac{17}{6}=[/latex]
  5. [latex]\dfrac{13}{3}=[/latex]
  6. [latex]\dfrac{20}{10}=[/latex]
  7. [latex]\dfrac{7}{4}=[/latex]

Exercise 4 Answers

  1. [latex]4\dfrac{1}{2}[/latex]
  2. [latex]1\dfrac{1}{10}[/latex]
  3. [latex]5[/latex]
  4. [latex]2\dfrac{5}{6}[/latex]
  5. [latex]4\dfrac{1}{3}[/latex]
  6. [latex]2[/latex]
  7. [latex]1\dfrac{3}{4}[/latex]

Renaming Mixed Numbers as Improper Fractions

This process will be used when you multiply and divide common fractions and “borrow” in subtraction.

Example F

Take the whole number 2.

Here are 2 equal shapes (see Figure 3.2.6).

 

Two squares.
Figure 3.2.6

The shapes are each divided into 3 parts (thirds) (see Figure 3.2.7).

 

Two squares, each divided into three parts.
Figure 3.2.7

How many thirds are there? 6 thirds.

[latex]2 =\dfrac{6}{3}[/latex]

Example G

Take the whole number 1.

Draw one shape (a circle or a box) (see Figure 3.2.8).

A circle.
Figure 3.2.8

Now, divide the shape into half (see Figure 3.2.9).

 

A circle divided into two parts.
Figure 3.2.9

How many halves are there?

[latex]1=\dfrac{2}{2}[/latex]

Have You Found the Shortcut?

The shortcut to rename a whole number as an improper fraction is to multiply the whole number by the denominator.

  • [latex]2 = \dfrac{}{4}\hspace{1cm}[/latex]
    • Each whole number has 4 equal parts (4 quarters) in it,
      • So [latex]2\text{ (whole numbers)}\times4\text{ (parts)} = 8\text{ parts}[/latex]
      • So [latex]2 = \dfrac{8}{4}[/latex]

     

  • [latex]6 = \dfrac{}{2}\hspace{1cm}[/latex]
    • Each whole number has 2 equal parts (2 halves),
      • So [latex]6\text{ (whole numbers)}\times2\text{ (parts)}=12\text{ parts}[/latex]
      • So [latex]6= \dfrac{12}{2}[/latex]

     

  • [latex]8 = \dfrac{}{3}[/latex]
    • [latex]8\times3=24[/latex]
      • So [latex]8 = \dfrac{24}{3}[/latex]

Until you are comfortable, draw a little sketch like you did in the example.

Exercise 5

Rename each whole number as an improper fraction using the denominator shown.

  1. [latex]6 = \dfrac{24}{4}[/latex],     [latex]2 = \dfrac{}{3}[/latex],       [latex]4 = \dfrac{}{3}[/latex],     [latex]8 = \dfrac{}{10}[/latex]
  2. [latex]7 = \dfrac{}{3}[/latex],     [latex]1 = \dfrac{}{4}[/latex],     [latex]6 = \dfrac{}{10}[/latex],     [latex]5 = \dfrac{}{6}[/latex]

Exercise 5 Answers

  1. [latex]\dfrac{24}{4}[/latex], [latex]\dfrac{6}{3}[/latex], [latex]\dfrac{12}{3}[/latex], [latex]\dfrac{80}{10}[/latex]
  2. [latex]\dfrac{21}{3}[/latex], [latex]\dfrac{4}{4}[/latex], [latex]\dfrac{60}{10}[/latex], [latex]\dfrac{30}{6}[/latex]

Now, let’s take this idea further. How can you rename a mixed number as an improper fraction?

Example H

Take the mixed number [latex]2\dfrac{1}{4}[/latex].

This is two whole things and part of a third whole thing.

Figure 3.2.10 shows three equal shapes divided into fourths.

 

Three squares each divided into fourths.
Figure 3.2.10

Shade in two whole shapes [latex]\dfrac{9}{4}[/latex] and [latex]\tfrac{1}{4}[/latex] of the third shape.

How many fourths have you shaded in all? 9 fourths

[latex]2\dfrac{1}{4} = \dfrac{9}{4}[/latex]

Example I

Take the mixed number [latex]1\dfrac{2}{3}[/latex]. This is one whole thing and part of a second whole thing.

Draw two equal shapes and divide them into thirds (see Figure 3.2.11).

Shade in one whole shape [latex]\dfrac{3}{3}[/latex] and [latex]\dfrac{2}{3}[/latex] of the second shape.

Two squares, each divided into three parts.
Figure 3.2.11

How many thirds have you shaded in all? _ thirds

[latex]1\dfrac{2}{3}=\dfrac{}{3}[/latex]

To rename a mixed number as an improper fraction, multiply the whole number by the denominator of the fraction and then add this to the numerator. Write the total as the new numerator over the denominator.

[latex]3\dfrac{1}{4}=\dfrac{}{4}[/latex]

[latex]3=\dfrac{12}{4}[/latex], so [latex]=3\dfrac{1}{4}=\dfrac{12}{4}+\dfrac{1}{4}=\dfrac{13}{4}[/latex]

[latex]2\dfrac{1}{2}\hspace{1cm}[/latex] [latex]2\times2=\dfrac{4}{2}+\dfrac{1}{2}=\dfrac{5}{2}[/latex]

Exercise 6

Rename each mixed number as an improper fraction.

  1. [latex]2\dfrac{4}{5} = \dfrac{14}{5}[/latex]
  2. [latex]8\dfrac{3}{8} = \dfrac{67}{8}[/latex]
  3. [latex]6\dfrac{5}{8} = \dfrac{}{8}[/latex]
  4. [latex]5\dfrac{1}{2} = \dfrac{}{2}[/latex]
  5. [latex]8\dfrac{4}{5} =[/latex]
  6. [latex]6\dfrac{1}{8} =[/latex]
  7. [latex]5\dfrac{3}{6} =[/latex]
  8. [latex]2\dfrac{7}{8} =[/latex]
  9. [latex]1\dfrac{8}{10}[/latex]
  10. [latex]3\dfrac{6}{8} =[/latex]

Exercise 6 Answers

  1. [latex]\dfrac{14}{5}[/latex]
  2. [latex]\dfrac{67}{8}[/latex]
  3. [latex]\dfrac{53}{8}[/latex]
  4. [latex]\dfrac{11}{2}[/latex]
  5. [latex]\dfrac{44}{5}[/latex]
  6. [latex]\dfrac{49}{8}[/latex]
  7. [latex]\dfrac{33}{6}[/latex]
  8. [latex]\dfrac{23}{8}[/latex]
  9. [latex]\dfrac{18}{10}[/latex]
  10. [latex]\dfrac{30}{8}[/latex]

To Say or Write a Mixed Number

If you want to say these strange looking fractions out loud, do as follows.

Write or say: the whole number + and + the fraction

  • [latex]3\dfrac{2}{5} =[/latex] three and two fifths
  • [latex]5\dfrac{1}{6} =[/latex] five and one sixth

Exercise 7

Write the following fractions as words.

  1. [latex]2\dfrac{1}{8}[/latex]
  2. [latex]4\dfrac{3}{4}[/latex]
  3. [latex]1\dfrac{1}{2}[/latex]
  4. [latex]3\dfrac{3}{4}[/latex]

Exercise 7 Answers

  1. two and one eighth
  2. four and three fourths (or four and three quarters)
  3. one and one half
  4. three and three fourths (or three and three quarters)

3.2: Practice Questions

  1. Write the improper fraction and the mixed number that describe the shaded part of the drawings in each question.
    1. 4 circles each divided into 3 parts. Three circles are fully shaded. One circle has one part shaded.
    2. Two shapes each divided into four parts. The first shape is fully shaded. The second shape has three parts shaded.

     

  2. Rename each improper fraction as an equivalent mixed number or whole number.
    1. [latex]\dfrac{9}{4}=[/latex]
    2. [latex]\dfrac{12}{3}=[/latex]
    3. [latex]\dfrac{5}{3}=[/latex]
    4. [latex]\dfrac{7}{2}=[/latex]

     

  3. Rename as improper fractions.
    1. [latex]3\dfrac{1}{2}=[/latex]
    2. [latex]4\dfrac{3}{8}=[/latex]
    3. [latex]1\dfrac{7}{8}=[/latex]
    4. [latex]2\dfrac{5}{6}=[/latex]

3.2: Practice Answers

  1. Write the improper fraction and the mixed number that describe the shaded part of the drawings in each question.
    1. [latex]\dfrac{10}{3} = 3\dfrac{1}{3}[/latex]
    2. [latex]\dfrac{7}{4} = 1\dfrac{3}{4}[/latex]

     

  2. Rename each improper fraction as an equivalent mixed number or whole number.
    1. [latex]2\dfrac{1}{4}[/latex]
    2. [latex]4[/latex]
    3. [latex]1\dfrac{2}{3}[/latex]
    4. [latex]3\dfrac{1}{2}[/latex]

     

  3. Rename as improper fractions
    1. [latex]\dfrac{7}{2}[/latex]
    2. [latex]\dfrac{35}{8}[/latex]
    3. [latex]\dfrac{15}{8}[/latex]
    4. [latex]\dfrac{17}{6}[/latex]

Attribution

All figures in this chapter are from Topic B: Common Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith, via BCcampus.

This chapter has been adapted from Topic B: Common Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition (BCcampus) by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith (2023), which is under a CC BY 4.0 license.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate PreAlgebra: Building Success Copyright © 2024 by Kim Tamblyn, TRU Open Press is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book