3.7: Multiplying Fractions
Example A
What is [latex]\dfrac{1}{4}[/latex] of 4? (Hint: Replace the word of with a × sign)
Figure 3.7.1 shows four equal shapes:

Shade in [latex]\dfrac{1}{4}[/latex] of the shapes. You should have one shape shaded.
You have just done this multiplication question:
[latex]\dfrac{1}{4}\times4=1[/latex] or [latex]\dfrac{1}{4}\text{ of }4=1[/latex]
Example B
What is [latex]\dfrac{2}{5}[/latex] of 5?
Step 1: Draw 5 equal shapes.
Step 2: Shade in [latex]\dfrac{2}{5}[/latex] of the shapes.
You should have shaded in two shapes.
[latex]\dfrac{2}{5}\times5=2[/latex] or [latex]\dfrac{2}{5}\text{ of }5=2[/latex]
Example C
What is [latex]\dfrac{1}{2}[/latex] of 10?
Step 1: Figure 3.7.2 shows 10 equal shapes:

Step 2: Shade in [latex]\dfrac{1}{2}[/latex] of the shapes.
Did you shade 5?
[latex]\dfrac{1}{2}\times10=2[/latex] or [latex]\dfrac{1}{2}\text{ of }10=5[/latex] of 10 = 5
Example D
What is [latex]\dfrac{1}{4}[/latex] of 8?

Step 1: Shade in [latex]\dfrac{1}{4}[/latex] of the shapes in Figure 3.7.3.
Step 2: Divide the 8 shapes into 4 equal groups.
Step 3: Shade 1 group.
[latex]\dfrac{1}{4}\times8=2[/latex] or [latex]\dfrac{1}{4}\text{ of }8=2[/latex]
Example E
What is [latex]\dfrac{2}{3}[/latex] of 6?

Step 1: Shade in [latex]\dfrac{2}{3}[/latex] of the shapes in Figure 3.7.4.
Step 2: Divide the 6 shapes into 3 equal groups.
Step 3: Shade 2 group.
[latex]\dfrac{2}{3}\times6=4[/latex]
These examples calculate a fraction of a whole number. Some everyday examples, with the answers, are listed:
- I burned [latex]\tfrac{1}{2}[/latex] of the hamburger patties. There were 8 patties. How many patties were burned?
- [latex]\tfrac{1}{2}[/latex] of 8 patties = [latex]\tfrac{1}{2}\times8=4[/latex] burned patties.
- Mary only finished [latex]\tfrac{3}{4}[/latex] of the test. The test had 20 questions. How many questions did Mary finish?
- [latex]\tfrac{3}{4}[/latex] of test = [latex]\tfrac{3}{4}[/latex] of 20 questions = [latex]\tfrac{3}{4}\times20=15[/latex] questions.
- [latex]\tfrac{1}{5}[/latex] of the employees have been laid off. There are 50 employees. How many have been laid off?
- [latex]\tfrac{1}{5}[/latex] of 50 employees = [latex]\tfrac{1}{5}\times50=10[/latex] employees laid off.
- We spend [latex]\tfrac{1}{4}[/latex] of our monthly take-home pay on rent. Our take-home pay is $1600. How much is the rent?
- [latex]\tfrac{1}{4}[/latex] of pay = [latex]\tfrac{1}{4}[/latex] of $1600 = [latex]\tfrac{1}{4}\times\$1600=\$400[/latex] on rent
Exercise 1
Write the multiplication equation you would use to find the fraction of the whole number. You do not have to calculate the answers.
- More than [latex]\dfrac{1}{3}[/latex] of the students are single parents. There are 27 students. How many students are single parents?
- We have ten houses on our street [latex]\dfrac{2}{5}[/latex] of the houses have cedar shake roofs. How many houses have cedar shake roofs?
- The guinea hen hatched 16 chicks. The ravens snatched [latex]\dfrac{3}{8}[/latex] of the chicks. How many chicks did the ravens take?
Exercise 1 Answers
- [latex]\dfrac{1}{3}\times27=9[/latex]
- [latex]\dfrac{2}{5}\times10=4[/latex]
- [latex]\dfrac{3}{8}\times16=6[/latex]
Now, let’s look at multiplying a fraction by a whole number:
- [latex]4\times\dfrac{1}{3}=[/latex]
- [latex]3\times\dfrac{4}{5}=[/latex]
- [latex]22\times\dfrac{1}{4}=[/latex]
The order of writing the multiplication equation will not change the product, but it does change how we understand what the numbers mean. Again, look at the examples:
Example F
[latex]4\times\dfrac{1}{2}[/latex] means you have four halves.
Imagine tomatoes cut in half and you have 4 halves (see Figure 3.7.5).
How many tomatoes would you have altogether?

4 halves = 2 tomatoes
[latex]4\times\dfrac{1}{2}=2[/latex]
Example G
[latex]3\times\dfrac{1}{4}[/latex] means that you have [latex]\dfrac{1}{4}[/latex] of something three times.
Imagine that you spent [latex]\dfrac{1}{4}[/latex] of an hour exercising in the morning, [latex]\dfrac{1}{4}[/latex] of an hour exercising after lunch, and [latex]\dfrac{1}{4}[/latex] of an hour exercising in the evening.
How long did you exercise?
[latex]3\times\dfrac{1}{4}[/latex] hour = [latex]\dfrac{3}{4}[/latex] hour = three quarters of an hour
Here are some everyday examples of multiplying a fraction by a whole number:
- There are six boxes of cereal open in the cupboard, and each one is 1/3 full. It is the same as having full boxes of cereal.
- [latex]6\times\tfrac{1}{3}[/latex] box of cereal = [latex]\tfrac{6}{3}[/latex] = 2 boxes of cereal
- We have three packs of ground beef that are [latex]\tfrac{1}{2}[/latex] full. How much meat is there altogether?
- [latex]3\times\tfrac{1}{2}[/latex] pack of meat = [latex]\tfrac{3}{2}[/latex] = [latex]1\tfrac{1}{2}[/latex] packs of meat.
- How much gas do we have for the motorboat? There are 4 jerry cans (cans for carrying gas), each about [latex]\tfrac{1}{4}[/latex] full.
- [latex]4\times\tfrac{1}{4}[/latex] cans of gas = [latex]\tfrac{4}{4}[/latex] = 1 can of gas.
Exercise 2
Write the multiplication equation you would use to multiply a fraction by a whole number. You do not have to calculate the answer.
- I should buy more shampoo, but this bathroom has five bottles of the stuff lying around! Each bottle is about [latex]\dfrac{1}{8}[/latex] full. How much shampoo is there altogether?
- When we double a recipe, we multiply each ingredient by 2. Double a recipe that uses [latex]\dfrac{1}{4}[/latex] teaspoon of nutmeg. How much nutmeg is needed?
Exercise 2 Answers
- [latex]5\times\dfrac{1}{8}=\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{4}\times2=\dfrac{1}{2}[/latex]
Multiplying a Whole Number and a Proper Fraction
Any whole number can be written with a denominator of 1. (This does not change the value of the whole number because a number divided by one is still the same whole number in the end.)
- 1 = [latex]\dfrac{1}{1}[/latex]
- 2 = [latex]\dfrac{2}{1}[/latex]
- 3 = [latex]\dfrac{3}{1}[/latex]
- 4 = [latex]\dfrac{4}{1}[/latex]
- 100 = [latex]\dfrac{100}{1}[/latex]
- and so on.
To multiply a whole number and a fraction, do the following:
- Write the whole number as a fraction with a denominator of 1.
- Multiply the numerator by the numerator.
- Multiply the denominator by the denominator.
- Simplify the product.
Example H
[latex]\dfrac{4}{6}\times6=[/latex]
Step 1: Write the whole number with a denominator of 1.
[latex]\dfrac{4}{5}\times\dfrac{6}{1}=[/latex]
Step 2: Multiply the numerators.
[latex]\dfrac{4}{5}\times\dfrac{6}{1}=\dfrac{24}{}[/latex]
Step 3: Multiply the denominators.
[latex]\dfrac{4}{5}\times\dfrac{6}{1}=\dfrac{24}{5}[/latex]
Step 4: Write your answer in lowest terms.
Since [latex]\begin{array}{r}4\\ 5\enclose{longdiv}{24}\\20\\ \hline 04\end{array}[/latex] [latex]\dfrac{24}{5}=4\dfrac{4}{5}[/latex] Then, [latex]\dfrac{4}{6}\times 6 = 4 \dfrac{4}{5}[/latex]
Example I
[latex]\dfrac{1}{2}\times 3=[/latex]
Step 1:
[latex]\dfrac{1}{2}\times\dfrac{3}{1}=[/latex]
Step 2 & 3:
[latex]\dfrac{1}{2}\times\dfrac{3}{1}[/latex] = [latex]\dfrac{3}{2}[/latex]
Step 4: Write your answer in lowest terms.
Since [latex]\begin{array}{r}1\\ 2\enclose{longdiv}{3}\\-2\\ \hline 1\end{array}[/latex] [latex]\dfrac{3}{2}[/latex] = [latex]1\dfrac{1}{2}[/latex] Then, [latex]\dfrac{1}{2}\times 3[/latex] = [latex]1\dfrac{1}{2}[/latex]
Example J
[latex]\dfrac{2}{3}\times4 =[/latex]
[latex]\dfrac{2}{3}\times\dfrac{4}{1}[/latex] = [latex]\dfrac{8}{3}[/latex] = [latex]2\dfrac{2}{3}[/latex]
[latex]\begin{array}{r}2\\ 3\enclose{longdiv}{8}\\-6\\ \hline 2\end{array}[/latex]
Example K
[latex]7 \times \dfrac{3}{4} =[/latex]
[latex]\dfrac{7}{1} \times \dfrac{3}{4} = \dfrac{21}{4} = 5\dfrac{1}{4}[/latex]
[latex]\begin{array}{r}5\\ 4\enclose{longdiv}{21}\\ −20\\ \hline 01\end{array}[/latex]
Exercise 3
Multiply these fractions. Write your answers in the lowest terms.
Examples:
- [latex]\dfrac{3}{5}\times10=\\\dfrac{3}{5}\times\dfrac{10}{1}=\dfrac{30}{5}=6\\\begin{array}{r}6\\ 5\enclose{longdiv}{30}\\ −30\\ \hline 0\end{array}[/latex]
- [latex]8\times\dfrac{1}{10}=\\\dfrac{8}{1}\times\dfrac{1}{10}=\dfrac{8\div2}{10\div2}=\dfrac{4}{5}[/latex]
- [latex]\dfrac{2}{3}\times9=[/latex]
- [latex]4\times\dfrac{1}{6}=[/latex]
- [latex]1\times\dfrac{3}{8}=[/latex]
- [latex]\dfrac{1}{2}\times5=[/latex]
- [latex]5\times\dfrac{2}{3}=[/latex]
- [latex]\dfrac{1}{2}\times8=[/latex]
- [latex]6\times\dfrac{1}{5}=[/latex]
- [latex]\dfrac{3}{2}\times12=[/latex]
- [latex]\dfrac{3}{8}\text{of }4 =[/latex]
- [latex]\dfrac{7}{8}\text{ of }3 =[/latex]
Exercise 3 Answers
- 6
- [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{3}{8}[/latex]
- [latex]2\dfrac{1}{2}[/latex]
- [latex]3\dfrac{1}{3}[/latex]
- 4
- [latex]1\dfrac{1}{5}[/latex]
- 18
- [latex]1\dfrac{1}{2}[/latex]
- [latex]2\dfrac{5}{8}[/latex]
Multiplying Common Fractions Together
To multiply common fractions, multiply the numerator times the numerator and then the denominator times the denominator and simplify the answer. (Write the answer in the lowest terms.)
The method is easy, but let’s look at what you’re doing.
Example L
[latex]\dfrac{1}{2}\times \dfrac{1}{2}= \dfrac{1}{2}[/latex] of [latex]\dfrac{1}{2}[/latex] =
Take an apple and cut it in half (see Figure 3.7.6).
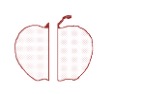
Now, cut one of the halves in half (see Figure 3.7.7). What fraction of the whole apple do you get?

You get [latex]\dfrac{1}{4}[/latex] of the apple.
[latex]\dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1}{4}[/latex]
Example M
[latex]\dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1}{2}[/latex] of [latex]\dfrac{1}{2}[/latex] =
You borrowed 3⁄4 of a bag of cement from your neighbour. You used 1⁄3 of the cement and gave the bag back to him. How much of your neighbour’s bag of cement did you use?
[latex]\dfrac{3}{4}[/latex] of a bag (see Figure 3.7.8)

[latex]\dfrac{2}{4}[/latex] of a bag (see Figure 3.7.9)

Use [latex]\dfrac{1}{3}[/latex] of this.
[latex]\dfrac{1}{3}[/latex] of [latex]\dfrac{3}{4} = \dfrac{1}{4}[/latex] of the bag used.
You used [latex]\dfrac{1}{4}[/latex] of a bag.
Example N
You are making a marinade to tenderize that cheap steak you bought. It calls for [latex]\dfrac{2}{3}[/latex] cup of beer. You only need [latex]\dfrac{1}{2}[/latex] of the amount the recipe makes, and it would be a shame to waste the beer. How much beer is needed?
[latex]\dfrac{1}{2}[/latex] of [latex]\dfrac{2}{3}[/latex] (see Figure 3.7.10)

[latex]\dfrac{1}{3}[/latex] of a cup (see Figure 3.7.11)
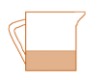
[latex]\dfrac{1}{3}[/latex] of a cup
[latex]\dfrac{1}{2}[/latex] of [latex]\dfrac{2}{3}[/latex] cup of beer = [latex]\dfrac{1}{2}[/latex] of [latex]\dfrac{2}{3}[/latex] cup of beer = [latex]\dfrac{1}{2}\times \dfrac{2}{3}[/latex] = [latex]\dfrac{2}{6}[/latex] = [latex]\dfrac{2}{6}[/latex] [latex]\dfrac{\div 2}{\div 2}[/latex] = [latex]\dfrac{1}{3}[/latex] cup of beer.
Exercise 4
Multiply these fractions. Write the answers in the lowest terms.
Example: [latex]\dfrac{1}{2}\times\dfrac{1}{2}[/latex] = [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{1}{2}\times\dfrac{4}{2}[/latex] =
- [latex]\dfrac{3}{5}\times\dfrac{2}{4}[/latex] =
- [latex]\dfrac{2}{5}\times\dfrac{3}{5}[/latex] =
- [latex]\dfrac{5}{6}\times\dfrac{1}{4}[/latex] =
- [latex]\dfrac{5}{10}\times\dfrac{1}{4}[/latex] =
- [latex]\dfrac{1}{4}\times\dfrac{1}{8}[/latex] =
- [latex]\dfrac{8}{10}\times\dfrac{2}{3}[/latex] =
Exercise 4 Answers
- 1
- [latex]\dfrac{3}{10}[/latex]
- [latex]\dfrac{6}{25}[/latex]
- [latex]\dfrac{5}{24}[/latex]
- [latex]\dfrac{1}{8}[/latex]
- [latex]\dfrac{1}{32}[/latex]
- [latex]\dfrac{8}{15}[/latex]
Simplify Before Multiplying
Multiplying common fractions can be much easier if you simplify before you multiply. In a multiplication question, any numerator and any denominator may be divided by a common factor. This is sometimes called cancelling.
For example:
[latex]\dfrac{2}{3}\times\dfrac{9}{10}[/latex] = [latex]\dfrac{5}{8}[/latex] = [latex]\dfrac{3}{8}[/latex]
Cancel any numerator with any denominator. Multiply all numerators together and then all denominators. Study this worked example:
Numerator 2 and denominator 8 have a common factor of 2, numerator 9 and denominator 3 have a common factor of 3, AND numerator 5 and denominator 10 have a common factor of 5:
[latex]\dfrac{\cancel{2}1}{\cancel{3}1} \times \dfrac{\cancel{9}3}{\cancel{10}2} \times \dfrac{\cancel{5}1}{\cancel{8}4} = \dfrac{3}{8}[/latex]
To simplify before multiplying:
- Look to see if any numerator and any denominator have Common Factors. Choose the Greatest Common Factor.
- Divide that numerator and that denominator by the Greatest Common Factor (GCF ). Be sure to cross out the old numerals and put in the lower terms.
- Multiply the numerators (Be sure to use the lower term!) and then the denominators.
- Simplify.
Example O
[latex]\dfrac{3}{4}\times\dfrac{1}{6}[/latex]
Step 1: Numerator 3 and denominator 6 have a common factor of 3.
Step 2:
[latex]\dfrac{\cancel{3}1}{4}\times\dfrac{1}{\cancel{6}2}[/latex]
[latex]3\div3 = 1 \text{ and } 6 \div 3 = 2[/latex]
Step 3:
[latex]\dfrac{\cancel{3}1}{4}\times\dfrac{1}{\cancel{6}2} = \dfrac{1}{8}[/latex]
Step 4: The answer is already in the lowest terms.
Example P
[latex]\dfrac{3}{4}\times\dfrac{8}{9}=[/latex]
Step 1: Numerator 3 and denominator 9 have a common factor of 3, AND numerator 8 and denominator 4 have common factors of 2 and 4. The GCF. is 4.
Step 2:
[latex]\dfrac{\cancel{3}1}{\cancel{4}1}\times\dfrac{\cancel{8}2}{\cancel{9}3}[/latex]
[latex]3\div3=1, 9\div3=3, 8\div4=2, \text{ and } 4\div4=1[/latex]
Step 3:
[latex]\dfrac{\cancel{3}1}{\cancel{4}1}\times\dfrac{\cancel{8}2}{\cancel{9}3}[/latex] = [latex]\dfrac{2}{3}[/latex]
Step 4: The answer is already in the lowest terms.
Example Q
[latex]\dfrac{3}{8}\times12 =[/latex]
[latex]\dfrac{3}{8}\times\dfrac{12}{1}[/latex]
Numerator 12 and denominator 8 have a GCF. of 4.
[latex]\dfrac{3}{\cancel{8}2}\times\dfrac{\cancel{12}3}{1}=\dfrac{9}{2}=4\dfrac{1}{2}[/latex]
It is easier to simplify (or cancel) before you multiply because the numbers are smaller, and the factors are easier to find.
You may make fewer multiplying mistakes, too.
Exercise 5
Find the products. Simplify before multiplying when possible.
Examples:
- [latex]\dfrac{5}{6}\times\dfrac{4}{5}= \\ \dfrac{\cancel{5}1}{\cancel{6}3} \times \dfrac{\cancel{4}2}{\cancel{5}1} = \dfrac{2}{3}[/latex]
- [latex]\dfrac{3}{5}\times\dfrac{5}{9} = \\ \dfrac{\cancel{3}1}{\cancel{5}1} \times \dfrac{\cancel{5}1}{\cancel{9}3} = \dfrac{1}{3}[/latex]
- [latex]\dfrac{3}{16}\times\dfrac{8}{9}[/latex] =
- [latex]\dfrac{2}{5}\times\dfrac{5}{8}[/latex] =
- [latex]\dfrac{4}{21}\times\dfrac{7}{8}[/latex] =
- [latex]\dfrac{9}{10}\times\dfrac{2}{3}[/latex] =
- [latex]\dfrac{2}{5}\times\dfrac{10}{7}[/latex] =
- [latex]\dfrac{3}{4}\times\dfrac{1}{12}[/latex] =
- [latex]\dfrac{8}{9}\times\dfrac{3}{4} =[/latex]
- [latex]\dfrac{1}{2}\times\dfrac{2}{5} \times \dfrac{5}{7} =[/latex]
- [latex]\dfrac{3}{5}\times\dfrac{2}{3} \times \dfrac{1}{2} =[/latex]
- [latex]2 \times \dfrac{3}{4}\times\dfrac{5}{12} =[/latex]
- [latex]\dfrac{4}{9}\times\dfrac{3}{5}\times \dfrac{15}{16} =[/latex]
- [latex]\dfrac{2}{3}\times\dfrac{3}{4} \times \dfrac{8}{9} =[/latex]
Exercise 5 Answers
- [latex]\dfrac{1}{6}[/latex]
- [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{1}{6}[/latex]
- [latex]\dfrac{3}{5}[/latex]
- [latex]\dfrac{4}{7}[/latex]
- [latex]\dfrac{1}{12}[/latex]
- [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{1}{7}[/latex]
- [latex]\dfrac{1}{5}[/latex]
- [latex]\dfrac{5}{8}[/latex]
- [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{4}{9}[/latex]
Multiplying Mixed Numbers
To multiply with a mixed number:
- Rename any mixed numbers as improper fractions.
- Write any whole number by itself as an improper fraction with a denominator of 1.
- Rewrite the question with the new improper fraction(s).
- Simplify (cancel).
- Multiply the numerator by the numerator. Multiply the denominator by the denominator.
- The answer will often be an improper fraction. Rename improper fractions as mixed numbers, and be sure any fraction is in the lowest terms.
Example R
[latex]2\dfrac{3}{4} \times \dfrac{1}{3} =[/latex]
Step 1:
[latex]2\dfrac{3}{4} = \dfrac{11}{4}[/latex]
Step 2: No whole numbers by themselves.
Step 3: Question is rewritten as [latex]\dfrac{11}{4}\times \dfrac{1}{3}[/latex].
Step 4: Simplify.
The fraction has no common factors, so it cannot be simplified.
Step 5:
[latex]\dfrac{11}{4} \times \dfrac{1}{3} = \dfrac{11}{12}[/latex]
Step 6: It is already in the lowest terms.
Example S
[latex]1\dfrac{1}{5}\times 2\dfrac{2}{3}[/latex]
Step 1:
[latex]1\dfrac{1}{5}=\dfrac{6}{5}[/latex] and [latex]2\dfrac{2}{3} = \dfrac{8}{3}[/latex]
Step 2: No whole numbers by themselves.
Step 3: Question is rewritten as [latex]\dfrac{6}{5}\times\dfrac{8}{3}[/latex].
Step 4 & 5:
[latex]\dfrac{\cancel{6}2}{5}\times\dfrac{8}{\cancel{3}1}=\dfrac{16}{5}[/latex] (an improper fraction)
Step 6:
[latex]\dfrac{16}{5} = 3 \dfrac{1}{5}[/latex] [latex]\begin{array}{r}3\\ 5\enclose{longdiv}{16}\\15\\ \hline 01\end{array}[/latex]
[latex]1\dfrac{1}{5}\times\dfrac2{2}{3}=3\dfrac{1}{5}[/latex]
Example T
[latex]4 \times 2\dfrac{5}{6}[/latex]
Step 1 and 2:
[latex]4 = \dfrac{4}{1}[/latex] and [latex]2 \dfrac{5}{6}= \dfrac{17}{6}[/latex]
Step 3: The question is rewritten as [latex]\dfrac{4}{1}\times\dfrac{17}{6}[/latex].
Step 4, 5 and 6:
[latex]4 \times 2\dfrac{5}{6}[/latex] = [latex]\dfrac{\cancel{4}2}{1}\times\dfrac{17}{\cancel{6}3}[/latex] = [latex]\dfrac{34}{3}[/latex] = [latex]11\dfrac{1}{3}[/latex]
Remember: Only skip steps when you are totally confident in your method. Writing out the steps will help you to get the answer right more often.
Exercise 6
Find the products.
Examples:
- [latex]2 \dfrac{1}{2}\times 6 = \\ \dfrac{7}{\cancel{2}1} \times \dfrac{\cancel{6}3}{1} = 21[/latex]
- [latex]3 \times \dfrac{1}{5}= \\ \dfrac{3}{1} \times \dfrac{6}{5} = \dfrac{18}{5} = 3 \dfrac{3}{5}[/latex]
- [latex]\dfrac{3}{14} \times 2\dfrac{1}{6} \times 12 =[/latex]
- [latex]3 \times 4\dfrac{1}{3} =[/latex]
- [latex]1\dfrac{2}{5} \times 15 =[/latex]
- [latex]3\dfrac{3}{8} \times 8 =[/latex]
- [latex]4 \times 2\dfrac{1}{2} =[/latex]
- [latex]2\dfrac{1}{4}\times 8 =[/latex]
Exercise 6 Answers
- [latex]5 \dfrac{4}{7}[/latex]
- 13
- 21
- 27
- 10
- 18
Exercise 7
This is extra practice if you feel you need it.
- [latex]1 \dfrac{ 1}{2}\times\dfrac{2}{3} =[/latex]
- [latex]1 \dfrac{1}{4}\times 3 \dfrac{1}{2} =[/latex]
- [latex]\dfrac{1}{3}\times 5 \dfrac{1}{2} =[/latex]
- [latex]1 \dfrac{1}{6}\times1 \dfrac{5}{7}=[/latex]
- [latex]\dfrac{1}{2}\times 2 \dfrac{1}{2}=[/latex]
- [latex]7 \dfrac{1}{4}\times 3 \dfrac{1}{3} =[/latex]
- [latex]7 \dfrac{1}{3}\times\dfrac{3}{8} =[/latex]
- [latex]2 \dfrac{1}{4}\times 3 \dfrac{1}{2} =[/latex]
Exercise 7 Answers
- 1
- [latex]4 \dfrac{3}{8}[/latex]
- [latex]1 \dfrac{5}{6}[/latex]
- 2
- [latex]1 \dfrac{1}{4}[/latex]
- [latex]24 \dfrac{1}{6}[/latex]
- [latex]2 \dfrac{3}{4}[/latex]
- [latex]7 \dfrac{7}{8}[/latex]
Problems Using Multiplication of Common Fractions
The following exercise gives some typical word problems for the multiplication of fractions. The type of wording is similar for decimals and common fractions.
Remember this important word:
A fraction of some number means to multiply.
Example:
- [latex]\dfrac{2}{3}[/latex] of her money means [latex]\dfrac{2}{3}[/latex] × amount of the money
- [latex]\dfrac{1}{4}[/latex] of the children means [latex]\dfrac{1}{4}[/latex]× number of children
These techniques may help you through the problem-solving steps when you’re working with common fractions:
- Look for keywords.
- Look for familiar patterns in the wording.
- Round fractions to whole numbers to estimate and to try to make sense of the problem.
- Draw a sketch or diagram of what the problem is describing.
Exercise 8
Solve the following word problems.
- Maria was angry with her children because they had eaten 2/3 of the 24 cupcakes she had made to take to a meeting. How many cupcakes did the kids eat?
- Double this recipe for Awesome Chocolate Chip Cookies.
- [latex]\dfrac{2}{3}[/latex] cup butter
- [latex]\dfrac{2}{3}[/latex] peanut butter
- [latex]\dfrac{5}{8}[/latex] white sugar
- [latex]\dfrac{5}{8}[/latex] brown sugar
- 2 eggs
- [latex]1\dfrac{3}{4}[/latex] tsp vanilla
- [latex]1\dfrac{1}{2}[/latex] cup flour
- 1 cup rolled oats
- 1 tsp baking soda
- [latex]\dfrac{1}{4}[/latex] tsp salt
- [latex]\dfrac{7}{8}[/latex] chocolate chips
Cream butter and peanut butter well, and blend in sugar. Beat in eggs and vanilla. Add dry ingredients, blending very thoroughly. Add chocolate chips and mix. Drop by spoonful onto the cookie sheet; cookies will flatten during cooking. Bake in 350 F. oven for 10 to 12 minutes.
- Marni is trying to gradually cut down on the amount of coffee she drinks. Right now she allows herself [latex]\dfrac{3}{4}[/latex] of a cup of coffee at breakfast, [latex]\dfrac{3}{4}[/latex] cup at morning break time, and [latex]\dfrac{3}{4}[/latex] cup at lunch and another [latex]\dfrac{3}{4}[/latex] cup after dinner. How many cups of coffee is she drinking per day right now?
- Sam’s truck uses [latex]\dfrac{1}{3}[/latex] of a tank of gas every time he drives to his girlfriend’s house. His tank holds 75 litres. How many litres of gas does he use to drive to his girlfriend’s place?
- If you do math for [latex]1\dfrac{1}{2}[/latex] hours every day you are at school, how many hours do you spend on math per month if you come to school twenty days in a month?
- David was complaining that his car insurance was the same price as [latex]\dfrac{7}{8}[/latex] of the cost of his car! His car cost $1200. What did he pay for car insurance?
- Justine was building a dog shed. She spent [latex]\dfrac{1}{3}[/latex] of an hour on the project every evening for 8 days in a row. How much time did she spend on the project?
Exercise 8 Answers
- 16 cupcakes
- Awesome Chocolate Chip Cookies (Doubled)
- [latex]1\dfrac{1}{3}[/latex]cup butter
- [latex]1\dfrac{1}{3}[/latex] cup peanut butter
- [latex]1\dfrac{1}{4}[/latex] cup white sugar
- [latex]1\dfrac{1}{4}[/latex] cup brown sugar
- 4 eggs
- [latex]3\dfrac{1}{2}[/latex] teaspoons vanilla
- 3 cups flour
- 2 cups rolled oats
- 2 teaspoons baking soda
- [latex]\dfrac{1}{2}[/latex] teaspoon salt
- [latex]1\dfrac{3}{4}[/latex] cup chocolate chips
- 3 cups
- 25 L
- 30 hours
- $1050.00
- 2 hours
3.7: Practice Questions
- Find the products.
- [latex]\dfrac{1}{4}\times\dfrac{3}{8}=[/latex]
- [latex]\dfrac{3}{8}\times\dfrac{5}{6} =[/latex]
- [latex]\dfrac{7}{9}\times\dfrac{3}{14}=[/latex]
- [latex]\dfrac{1}{4}\times 12 =[/latex]
- [latex]5\times\dfrac{4}{9}=[/latex]
- [latex]1\dfrac{1}{4}\times\dfrac{4}{5}=[/latex]
- [latex]\dfrac{3}{5} \times 7\dfrac{2}{9}=[/latex]
- [latex]6\times 1\dfrac{2}{3}=[/latex]
- [latex]1\dfrac{1}{2}\times 1\dfrac{3}{5}=[/latex]
- [latex]2\dfrac{7}{8}\times1\dfrac{9}{10}=[/latex]
- Solve the following word problems.
- Frank is hosting a big party. He needs to multiply his favourite tomato sauce by five to make enough to serve his guests. Five times this recipe for him.
-
- [latex]1\dfrac{1}{2}[/latex] Tbsp Olive Oil;
- 1 Onions;
- [latex]1\dfrac{1}{2}[/latex] tsp salt;
- 2 bay leaves;
- 6 garlic cloves;
- [latex]1\dfrac{1}{3}[/latex] tsp red chili flakes;
- [latex]1\dfrac{3}{4}[/latex]diced tomatoes;
- [latex]1\dfrac{1}{4}[/latex] brown sugar;
-
- Joey practices [latex]\dfrac{3}{4}[/latex] of an hour each day. How much time does he spend practicing each week?
- A Haida longhouse measures [latex]15\dfrac{1}{4}[/latex] m by [latex]18\dfrac{1}{3}[/latex] m. What area of land does it cover?
- Find the area of the rectangle.
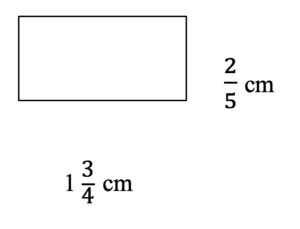
- Frank is hosting a big party. He needs to multiply his favourite tomato sauce by five to make enough to serve his guests. Five times this recipe for him.
3.7: Practice Answers
- Find the products.
- [latex]\dfrac{3}{32}[/latex]
- [latex]\dfrac{5}{2}[/latex]
- [latex]\dfrac{1}{6}[/latex]
- 3
- [latex]2\dfrac{3}{32}[/latex]
- 1
- [latex]4\dfrac{1}{3}[/latex]
- 10
- [latex]2\dfrac{2}{5}[/latex]
- [latex]5\dfrac{37}{80}[/latex]
- Solve the following word problems.
- Five times this recipe:
- [latex]7\dfrac{1}{2}[/latex] Tbsp Olive Oil;
- 5 Onions;
- [latex]2\dfrac{1}{2}[/latex] tsp salt;
- 10 bay leaves;
- 30 garlic cloves;
- [latex]1\dfrac{2}{3}[/latex] tsp red chili flakes;
- [latex]8\dfrac{3}{4}[/latex] diced tomatoes;
- [latex]6\dfrac{1}{4}[/latex] brown sugar;
- [latex]5\dfrac{1}{4}[/latex]
- [latex]279\dfrac{7}{12}[/latex] m2 in area
- [latex]\dfrac{7}{10}[/latex] cm
- Five times this recipe:
Attribution
All figures in this chapter are from Topic A: Multiplying Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith, via BCcampus.
This chapter has been adapted from Topic A: Multiplying Fractions in Adult Literacy Fundamental Mathematics: Book 5 – 2nd Edition (BCcampus) by Liz Girard, Wendy Tagami, and Leanne Caillier-Smith (2023), which is under a CC BY 4.0 license.

